Second-Order Sensitivity Analysis of Uncollided Particle Contributions to Radiation Detector Responses
- Authors:
-
- Univ. of South Carolina, Columbia, SC (United States)
- Los Alamos National Lab. (LANL), Los Alamos, NM (United States)
- Publication Date:
- Research Org.:
- Los Alamos National Laboratory (LANL), Los Alamos, NM (United States)
- Sponsoring Org.:
- USDOE National Nuclear Security Administration (NNSA), Office of Defense Nuclear Nonproliferation
- OSTI Identifier:
- 1441310
- Alternate Identifier(s):
- OSTI ID: 1489987
- Report Number(s):
- LA-UR-17-28959; LA-UR-18-24819
Journal ID: ISSN 0029-5639; TRN: US1900890
- Grant/Contract Number:
- AC52-06NA25396; 89233218CNA000001
- Resource Type:
- Accepted Manuscript
- Journal Name:
- Nuclear Science and Engineering
- Additional Journal Information:
- Journal Volume: 190; Journal Issue: 2; Journal ID: ISSN 0029-5639
- Publisher:
- American Nuclear Society - Taylor & Francis
- Country of Publication:
- United States
- Language:
- English
- Subject:
- 73 NUCLEAR PHYSICS AND RADIATION PHYSICS; second-order adjoint sensitivity analysis; particle and radiation transport; response variance and skewness
Citation Formats
Cacuci, Dan G., and Favorite, Jeffrey A. Second-Order Sensitivity Analysis of Uncollided Particle Contributions to Radiation Detector Responses. United States: N. p., 2018.
Web. doi:10.1080/00295639.2018.1426899.
Cacuci, Dan G., & Favorite, Jeffrey A. Second-Order Sensitivity Analysis of Uncollided Particle Contributions to Radiation Detector Responses. United States. https://doi.org/10.1080/00295639.2018.1426899
Cacuci, Dan G., and Favorite, Jeffrey A. Fri .
"Second-Order Sensitivity Analysis of Uncollided Particle Contributions to Radiation Detector Responses". United States. https://doi.org/10.1080/00295639.2018.1426899. https://www.osti.gov/servlets/purl/1441310.
@article{osti_1441310,
title = {Second-Order Sensitivity Analysis of Uncollided Particle Contributions to Radiation Detector Responses},
author = {Cacuci, Dan G. and Favorite, Jeffrey A.},
abstractNote = {},
doi = {10.1080/00295639.2018.1426899},
journal = {Nuclear Science and Engineering},
number = 2,
volume = 190,
place = {United States},
year = {Fri Apr 06 00:00:00 EDT 2018},
month = {Fri Apr 06 00:00:00 EDT 2018}
}
Free Publicly Available Full Text
Publisher's Version of Record
Other availability
Cited by: 10 works
Citation information provided by
Web of Science
Web of Science
Figures / Tables:
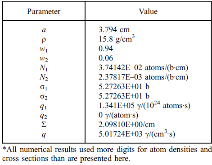 TABLE I: Sphere and Material Parameters
TABLE I: Sphere and Material Parameters
All figures and tables
(21 total)
Save to My Library
You must Sign In or Create an Account in order to save documents to your library.
Works referenced in this record:
Sensitivity theory for nonlinear systems. II. Extensions to additional classes of responses
journal, December 1981
- Cacuci, Dan G.
- Journal of Mathematical Physics, Vol. 22, Issue 12
Adjoint-based constant-mass partial derivatives
journal, December 2017
- Favorite, Jeffrey A.
- Annals of Nuclear Energy, Vol. 110
Second-order adjoint sensitivity analysis methodology (2nd-ASAM) for computing exactly and efficiently first- and second-order sensitivities in large-scale linear systems: I. Computational methodology
journal, March 2015
- Cacuci, Dan G.
- Journal of Computational Physics, Vol. 284
Second-order adjoint sensitivity analysis methodology (2nd-ASAM) for computing exactly and efficiently first- and second-order sensitivities in large-scale linear systems: II. Illustrative application to a paradigm particle diffusion problem
journal, March 2015
- Cacuci, Dan G.
- Journal of Computational Physics, Vol. 284
Sensitivity theory for nonlinear systems. I. Nonlinear functional analysis approach
journal, December 1981
- Cacuci, Dan G.
- Journal of Mathematical Physics, Vol. 22, Issue 12
Computational Evaluation of Neutron Multiplicity Measurements of Polyethylene-Reflected Plutonium Metal
journal, February 2014
- Miller, E. C.; Mattingly, J. K.; Clarke, S. D.
- Nuclear Science and Engineering, Vol. 176, Issue 2
Polyethylene-reflected plutonium metal sphere : subcritical neutron and gamma measurements.
report, November 2009
- Mattingly, John K.
Works referencing / citing this record:
Application of the Second-Order Comprehensive Adjoint Sensitivity Analysis Methodology to Compute First- and Second-Order Sensitivities of Flux Functionals in a Multiplying System with Source
journal, January 2019
- Cacuci, Dan Gabriel
- Nuclear Science and Engineering, Vol. 193, Issue 6
Figures / Tables found in this record:
Figures/Tables have been extracted from DOE-funded journal article accepted manuscripts.

 Search WorldCat to find libraries that may hold this journal
Search WorldCat to find libraries that may hold this journal