Integrable Time-Dependent Quantum Hamiltonians
Abstract
Here we formulate a set of conditions under which the nonstationary Schrödinger equation with a time-dependent Hamiltonian is exactly solvable analytically. The main requirement is the existence of a non-Abelian gauge field with zero curvature in the space of system parameters. Known solvable multistate Landau-Zener models satisfy these conditions. Our method provides a strategy to incorporate time dependence into various quantum integrable models while maintaining their integrability. Finally, we also validate some prior conjectures, including the solution of the driven generalized Tavis-Cummings model.
- Authors:
-
- Los Alamos National Lab. (LANL), Los Alamos, NM (United States)
- Rutgers Univ., Piscataway, NJ (United States). Center for Materials Theory. Dept. of Physics and Astronomy
- Wayne State Univ., Detroit, MI (United States). Dept. of Chemistry. Dept. of Mathematics
- Los Alamos National Lab. (LANL), Los Alamos, NM (United States); Rutgers Univ., Piscataway, NJ (United States). Center for Materials Theory. Dept. of Physics and Astronomy
- Los Alamos National Lab. (LANL), Los Alamos, NM (United States); Texas A & M Univ., College Station, TX (United States). Dept. of Physics
- Publication Date:
- Research Org.:
- Los Alamos National Laboratory (LANL), Los Alamos, NM (United States); Rutgers Univ., Piscataway, NJ (United States); Wayne State Univ., Detroit, MI (United States)
- Sponsoring Org.:
- USDOE National Nuclear Security Administration (NNSA); LANL Laboratory Directed Research and Development (LDRD) Program; National Science Foundation (NSF)
- OSTI Identifier:
- 1482922
- Alternate Identifier(s):
- OSTI ID: 1436899
- Report Number(s):
- LA-UR-17-28411
Journal ID: ISSN 0031-9007
- Grant/Contract Number:
- AC52-06NA25396; DMR-1609829; CHE-1111350
- Resource Type:
- Accepted Manuscript
- Journal Name:
- Physical Review Letters
- Additional Journal Information:
- Journal Volume: 120; Journal Issue: 19; Journal ID: ISSN 0031-9007
- Publisher:
- American Physical Society (APS)
- Country of Publication:
- United States
- Language:
- English
- Subject:
- 71 CLASSICAL AND QUANTUM MECHANICS, GENERAL PHYSICS; coherent control; mathematical physics; quantum theory; scattering theory
Citation Formats
Sinitsyn, Nikolai A., Yuzbashyan, Emil A., Chernyak, Vladimir Y., Patra, Aniket, and Sun, Chen. Integrable Time-Dependent Quantum Hamiltonians. United States: N. p., 2018.
Web. doi:10.1103/PhysRevLett.120.190402.
Sinitsyn, Nikolai A., Yuzbashyan, Emil A., Chernyak, Vladimir Y., Patra, Aniket, & Sun, Chen. Integrable Time-Dependent Quantum Hamiltonians. United States. https://doi.org/10.1103/PhysRevLett.120.190402
Sinitsyn, Nikolai A., Yuzbashyan, Emil A., Chernyak, Vladimir Y., Patra, Aniket, and Sun, Chen. Fri .
"Integrable Time-Dependent Quantum Hamiltonians". United States. https://doi.org/10.1103/PhysRevLett.120.190402. https://www.osti.gov/servlets/purl/1482922.
@article{osti_1482922,
title = {Integrable Time-Dependent Quantum Hamiltonians},
author = {Sinitsyn, Nikolai A. and Yuzbashyan, Emil A. and Chernyak, Vladimir Y. and Patra, Aniket and Sun, Chen},
abstractNote = {Here we formulate a set of conditions under which the nonstationary Schrödinger equation with a time-dependent Hamiltonian is exactly solvable analytically. The main requirement is the existence of a non-Abelian gauge field with zero curvature in the space of system parameters. Known solvable multistate Landau-Zener models satisfy these conditions. Our method provides a strategy to incorporate time dependence into various quantum integrable models while maintaining their integrability. Finally, we also validate some prior conjectures, including the solution of the driven generalized Tavis-Cummings model.},
doi = {10.1103/PhysRevLett.120.190402},
journal = {Physical Review Letters},
number = 19,
volume = 120,
place = {United States},
year = {Fri May 11 00:00:00 EDT 2018},
month = {Fri May 11 00:00:00 EDT 2018}
}
Free Publicly Available Full Text
Publisher's Version of Record
Other availability
Cited by: 37 works
Citation information provided by
Web of Science
Web of Science
Figures / Tables:
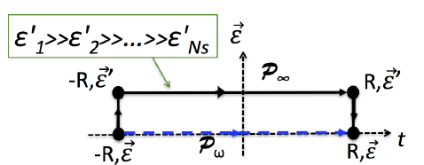 FIG. 1: (color online) Paths in the space of parameters ϵj and time used to evaluate transition probabilities for the driven generalized Tavis-Cummings model (9), ω = t. On Pω, ω changes from –R to +R, all ϵj are fixed. Since this model is a part of a commuting familymore »
FIG. 1: (color online) Paths in the space of parameters ϵj and time used to evaluate transition probabilities for the driven generalized Tavis-Cummings model (9), ω = t. On Pω, ω changes from –R to +R, all ϵj are fixed. Since this model is a part of a commuting familymore »
All figures and tables
(4 total)
Save to My Library
You must Sign In or Create an Account in order to save documents to your library.
Works referenced in this record:
Interplay of charge and spin coherence in Landau-Zener-Stückelberg-Majorana interferometry
journal, June 2013
- Ribeiro, Hugo; Petta, J. R.; Burkard, Guido
- Physical Review B, Vol. 87, Issue 23
Relaxation and Prethermalization in an Isolated Quantum System
journal, September 2012
- Gring, M.; Kuhnert, M.; Langen, T.
- Science, Vol. 337, Issue 6100
Exact out-of-equilibrium central spin dynamics from integrability
journal, April 2014
- Fioretto, Davide; Caux, Jean-Sébastien; Gritsev, Vladimir
- New Journal of Physics, Vol. 16, Issue 4
Dynamics of a Quantum Phase Transition: Exact Solution of the Quantum Ising Model
journal, December 2005
- Dziarmaga, Jacek
- Physical Review Letters, Vol. 95, Issue 24
Quantum simulation of the Kibble-Zurek mechanism using a semiconductor electron charge qubit
journal, February 2014
- Wang, Li; Zhou, Cheng; Tu, Tao
- Physical Review A, Vol. 89, Issue 2
Quantum annealing with all-to-all connected nonlinear oscillators
journal, June 2017
- Puri, Shruti; Andersen, Christian Kraglund; Grimsmo, Arne L.
- Nature Communications, Vol. 8, Issue 1
Landau-Zener extension of the Tavis-Cummings model: Structure of the solution
journal, September 2016
- Sun, Chen; Sinitsyn, Nikolai A.
- Physical Review A, Vol. 94, Issue 3
Classification of parameter-dependent quantum integrable models, their parameterization, exact solution and other properties
journal, September 2011
- Owusu, Haile K.; Yuzbashyan, Emil A.
- Journal of Physics A: Mathematical and Theoretical, Vol. 44, Issue 39
Integrability of the pairing hamiltonian
journal, October 1997
- Cambiaggio, M. C.; Rivas, A. M. F.; Saraceno, M.
- Nuclear Physics A, Vol. 624, Issue 2
Experiments on spontaneous vortex formation in Josephson tunnel junctions
journal, October 2006
- Monaco, R.; Aaroe, M.; Mygind, J.
- Physical Review B, Vol. 74, Issue 14
Dynamical Control of Matter-Wave Tunneling in Periodic Potentials
journal, November 2007
- Lignier, H.; Sias, C.; Ciampini, D.
- Physical Review Letters, Vol. 99, Issue 22
Ultrahigh-Resolution NMR Spectroscopy
journal, May 2014
- Foroozandeh, Mohammadali; Adams, Ralph W.; Meharry, Nicola J.
- Angewandte Chemie International Edition, Vol. 53, Issue 27
Coherent control of three-spin states in a triple quantum dot
journal, November 2011
- Gaudreau, L.; Granger, G.; Kam, A.
- Nature Physics, Vol. 8, Issue 1
Quantum Spin Dynamics of Mode-Squeezed Luttinger Liquids in Two-Component Atomic Gases
journal, April 2008
- Widera, Artur; Trotzky, Stefan; Cheinet, Patrick
- Physical Review Letters, Vol. 100, Issue 14
Exact analytical solution of the N -level Landau - Zener-type bow-tie model
journal, October 1997
- Ostrovsky, Valentine N.; Nakamura, Hiroki
- Journal of Physics A: Mathematical and General, Vol. 30, Issue 19
Solvable four-state Landau-Zener model of two interacting qubits with path interference
journal, November 2015
- Sinitsyn, N. A.
- Physical Review B, Vol. 92, Issue 20
Nonadiabatic Landau-Zener tunneling in Fe 8 molecular nanomagnets
journal, May 2000
- Wernsdorfer, W.; Sessoli, R.; Caneschi, A.
- Europhysics Letters (EPL), Vol. 50, Issue 4
Spontaneous vortices in the formation of Bose–Einstein condensates
journal, October 2008
- Weiler, Chad N.; Neely, Tyler W.; Scherer, David R.
- Nature, Vol. 455, Issue 7215
Current algebra and Wess-Zumino model in two dimensions
journal, December 1984
- Knizhnik, V. G.; Zamolodchikov, A. B.
- Nuclear Physics B, Vol. 247, Issue 1
Quantum integrability in the multistate Landau–Zener problem
journal, May 2015
- Patra, A.; Yuzbashyan, E. A.
- Journal of Physics A: Mathematical and Theoretical, Vol. 48, Issue 24
The model of a level crossing with a Coulomb band: exact probabilities of nonadiabatic transitions
journal, April 2014
- Lin, J.; Sinitsyn, N. A.
- Journal of Physics A: Mathematical and Theoretical, Vol. 47, Issue 17
Landau-Zener transitions in a linear chain
journal, April 2002
- Pokrovsky, V. L.; Sinitsyn, N. A.
- Physical Review B, Vol. 65, Issue 15
Non-Adiabatic Crossing of Energy Levels
journal, September 1932
- Zener, C.
- Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, Vol. 137, Issue 833
Quantum Integrability in Systems with Finite Number of Levels
journal, January 2013
- Yuzbashyan, Emil A.; Shastry, B. Sriram
- Journal of Statistical Physics, Vol. 150, Issue 4
Higgs Amplitude Mode in the BCS Superconductors Induced by Terahertz Pulse Excitation
journal, July 2013
- Matsunaga, Ryusuke; Hamada, Yuki I.; Makise, Kazumasa
- Physical Review Letters, Vol. 111, Issue 5
Many-body Landau–Zener dynamics in coupled one-dimensional Bose liquids
journal, October 2010
- Chen, Yu-Ao; Huber, Sebastian D.; Trotzky, Stefan
- Nature Physics, Vol. 7, Issue 1
Quantum Inverse Scattering Method and Correlation Functions
book, January 2010
- Korepin, V. E.; Bogoliubov, N. M.; Izergin, A. G.
- Cambridge University Press
Characterization of Qubit Dephasing by Landau-Zener-Stückelberg-Majorana Interferometry
journal, March 2014
- Forster, F.; Petersen, G.; Manus, S.
- Physical Review Letters, Vol. 112, Issue 11
Adiabatic perturbation theory and geometry of periodically-driven systems
journal, May 2017
- Weinberg, Phillip; Bukov, Marin; D’Alessio, Luca
- Physics Reports, Vol. 688
Integrable dynamics of coupled Fermi-Bose condensates
journal, October 2005
- Yuzbashyan, Emil A.; Kuznetsov, Vadim B.; Altshuler, Boris L.
- Physical Review B, Vol. 72, Issue 14
Ultrafast universal quantum control of a quantum-dot charge qubit using Landau–Zener–Stückelberg interference
journal, January 2013
- Cao, Gang; Li, Hai-Ou; Tu, Tao
- Nature Communications, Vol. 4, Issue 1
Multiparticle Landau-Zener problem: Application to quantum dots
journal, November 2002
- Sinitsyn, N. A.
- Physical Review B, Vol. 66, Issue 20
Many Body Generalization of the Landau-Zener Problem
journal, February 2008
- Altland, Alexander; Gurarie, V.
- Physical Review Letters, Vol. 100, Issue 6
The link between integrability, level crossings and exact solution in quantum models
journal, December 2008
- Owusu, H. K.; Wagh, K.; Yuzbashyan, E. A.
- Journal of Physics A: Mathematical and Theoretical, Vol. 42, Issue 3
Condensation of Pairs of Fermionic Atoms near a Feshbach Resonance
journal, March 2004
- Zwierlein, M. W.; Stan, C. A.; Schunck, C. H.
- Physical Review Letters, Vol. 92, Issue 12
Beautiful Models: 70 Years of Exactly Solved Quantum Many-Body Problems
book, June 2004
- Sutherland, Bill
Multipath interference in a multistate Landau-Zener-type model
journal, February 2000
- Demkov, Yu. N.; Ostrovsky, V. N.
- Physical Review A, Vol. 61, Issue 3
Gauging a Quantum Heat Bath with Dissipative Landau-Zener Transitions
journal, November 2006
- Wubs, Martijn; Saito, Keiji; Kohler, Sigmund
- Physical Review Letters, Vol. 97, Issue 20
Multi-time Schrödinger equations cannot contain interaction potentials
journal, March 2014
- Petrat, Sören; Tumulka, Roderich
- Journal of Mathematical Physics, Vol. 55, Issue 3
Nonadiabatic Transitions in Exactly Solvable Quantum Mechanical Multichannel Model: Role of Level Curvature and Counterintuitive Behavior
journal, April 2013
- Sinitsyn, N. A.
- Physical Review Letters, Vol. 110, Issue 15
Quantum quench phase diagrams of an -wave BCS-BEC condensate
journal, March 2015
- Yuzbashyan, E. A.; Dzero, M.; Gurarie, V.
- Physical Review A, Vol. 91, Issue 3
Nonadiabaticity and large fluctuations in a many-particle Landau-Zener problem
journal, April 2009
- Altland, Alexander; Gurarie, V.; Kriecherbauer, T.
- Physical Review A, Vol. 79, Issue 4
The quest for solvable multistate Landau-Zener models
journal, May 2017
- Sinitsyn, Nikolai A.; Chernyak, Vladimir Y.
- Journal of Physics A: Mathematical and Theoretical, Vol. 50, Issue 25
Exact transition probabilities in a 6-state Landau–Zener system with path interference
journal, April 2015
- Sinitsyn, N. A.
- Journal of Physics A: Mathematical and Theoretical, Vol. 48, Issue 19
Quenching of dynamic nuclear polarization by spin–orbit coupling in GaAs quantum dots
journal, July 2015
- Nichol, John M.; Harvey, Shannon P.; Shulman, Michael D.
- Nature Communications, Vol. 6, Issue 1
Boundary Wess-Zumino-Novikov-Witten model from the pairing Hamiltonian
journal, December 2010
- Sedrakyan, Tigran A.; Galitski, Victor
- Physical Review B, Vol. 82, Issue 21
Conformal field theory and the exact solution of the BCS Hamiltonian
journal, April 2000
- Sierra, Germán
- Nuclear Physics B, Vol. 572, Issue 3
Observation of Resonance Condensation of Fermionic Atom Pairs
journal, January 2004
- Regal, C. A.; Greiner, M.; Jin, D. S.
- Physical Review Letters, Vol. 92, Issue 4
Complete Generalized Gibbs Ensembles in an Interacting Theory
journal, October 2015
- Ilievski, E.; De Nardis, J.; Wouters, B.
- Physical Review Letters, Vol. 115, Issue 15
Solvable multistate model of Landau-Zener transitions in cavity QED
journal, June 2016
- Sinitsyn, Nikolai A.; Li, Fuxiang
- Physical Review A, Vol. 93, Issue 6
Quantum Tunneling in Half-Integer Spin Systems
journal, September 2001
- Miyashita, S.; Nagaosa, N.
- Progress of Theoretical Physics, Vol. 106, Issue 3
Off-shell Bethe ansatz equations and N-point correlators in the SU(2) WZNW theory
journal, December 1993
- Babujian, H. M.
- Journal of Physics A: Mathematical and General, Vol. 26, Issue 23
S-matrix for generalized Landau-Zener problem
journal, March 1993
- Brundobler, S.; Elser, Veit
- Journal of Physics A: Mathematical and General, Vol. 26, Issue 5
SU(3) Landau-Zener interferometry
journal, December 2013
- Kiselev, M. N.; Kikoin, K.; Kenmoe, M. B.
- EPL (Europhysics Letters), Vol. 104, Issue 5
Exact results for models of multichannel quantum nonadiabatic transitions
journal, December 2014
- Sinitsyn, N. A.
- Physical Review A, Vol. 90, Issue 6
Probing the relaxation towards equilibrium in an isolated strongly correlated one-dimensional Bose gas
journal, February 2012
- Trotzky, S.; Chen, Y-A.; Flesch, A.
- Nature Physics, Vol. 8, Issue 4
The exact solution of the multistate Landau-Zener type model: the generalized bow-tie model
journal, June 2001
- Demkov, Yu N.; Ostrovsky, V. N.
- Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 34, Issue 12
A quantum Newton's cradle
journal, April 2006
- Kinoshita, Toshiya; Wenger, Trevor; Weiss, David S.
- Nature, Vol. 440, Issue 7086
Ultrahigh-Resolution NMR Spectroscopy
journal, May 2014
- Foroozandeh, Mohammadali; Adams, Ralph W.; Meharry, Nicola J.
- Angewandte Chemie, Vol. 126, Issue 27
Dynamical control of matter-wave tunneling in periodic potentials
text, January 2007
- Lignier, H.; Sias, C.; Ciampini, D.
- arXiv
Quantum Spin Dynamics of Mode-Squeezed Luttinger Liquids in Two-Component Atomic Gases
text, January 2007
- Widera, Artur; Trotzky, Stefan; Cheinet, Patrick
- arXiv
Non-adiabacity and large flucutations in a many particle Landau Zener problem
text, January 2008
- Altland, A.; Gurarie, V.; Kriecherbauer, T.
- arXiv
Boundary Wess-Zumino-Novikov-Witten Model from the Pairing Hamiltonian
text, January 2010
- Sedrakyan, Tigran A.; Galitski, Victor
- arXiv
Classification of Parameter-Dependent Quantum Integrable Models, Their Parameterization, Exact Solution, and Other Properties
text, January 2011
- Owusu, Haile K.; Yuzbashyan, Emil A.
- arXiv
Coherent control of three-spin states in a triple quantum dot
text, January 2011
- Gaudreau, L.; Granger, G.; Kam, A.
- arXiv
Quantum quench phase diagrams of an s-wave BCS-BEC condensate
text, January 2014
- Yuzbashyan, Emil A.; Dzero, Maxim; Gurarie, Victor
- arXiv
Complete Generalized Gibbs Ensemble in an interacting Theory
text, January 2015
- Ilievski, Enej; De Nardis, Jacopo; Wouters, Bram
- arXiv
Solvable multistate model of Landau-Zener transitions in cavity QED
text, January 2016
- Sinitsyn, Nikolai A.; Li, Fuxiang
- arXiv
Nonadiabatic Landau Zener tunneling in Fe_8 molecular nanomagnets
text, January 2000
- Wernsdorfer, W.; Sessoli, R.; Caneschi, A.
- arXiv
Landau-Zener transitions in a linear chain
text, January 2001
- Pokrovsky, V. L.; Sinitsyn, N. A.
- arXiv
Observation of resonance condensation of fermionic atom pairs
text, January 2004
- Regal, C. A.; Greiner, M.; Jin, D. S.
- arXiv
Dynamics of quantum phase transition: exact solution in quantum Ising model
text, January 2005
- Dziarmaga, Jacek
- arXiv
New Experiments for Spontaneous Vortex Formation in Josephson Tunnel Junctions
text, January 2006
- Monaco, R.; Aaroe, M.; Myging, J.
- arXiv
Gauging a quantum heat bath with dissipative Landau-Zener transitions
text, January 2006
- Wubs, Martijn; Saito, Keiji; Kohler, Sigmund
- arXiv
Off-Shell Bethe Ansatz Equation and N-point Correlators in the SU(2) WZNW Theory
text, January 1993
- Baboujian, H. M.
- arXiv
Conformal Field Theory and the Exact Solution of the BCS Hamiltonian
text, January 1999
- Sierra, German
- arXiv
Integrability of the pairing hamiltonian
text, January 1997
- Cambiaggio, M. C.; Rivas, A. M. F.; Saraceno, M.
- arXiv
Works referencing / citing this record:
A large class of solvable multistate Landau–Zener models and quantum integrability
journal, May 2018
- Chernyak, Vladimir Y.; Sinitsyn, Nikolai A.; Sun, Chen
- Journal of Physics A: Mathematical and Theoretical, Vol. 51, Issue 24
Detuning-induced robustness of a three-state Landau-Zener model against dissipation
journal, June 2019
- Militello, Benedetto
- Physical Review A, Vol. 99, Issue 6
Resonant Transitions Due to Changing Boundaries
journal, June 2019
- Anzà, Fabio; Messina, Antonino; Militello, Benedetto
- Open Systems & Information Dynamics, Vol. 26, Issue 02
Counterdiabatic Hamiltonians for multistate Landau-Zener problem
journal, January 2018
- Nishimura, Kohji; Takahashi, Kazutaka
- SciPost Physics, Vol. 5, Issue 3
Resonant transitions due to changing boundaries
text, January 2015
- Anzà, F.; Messina, A.; Militello, B.
- arXiv
Integrable Floquet Hamiltonian for a Periodically Tilted 1D Gas
text, January 2019
- Colcelli, Andrea; Mussardo, Giuseppe; Sierra, German
- arXiv
Figures / Tables found in this record:
Figures/Tables have been extracted from DOE-funded journal article accepted manuscripts.

 Search WorldCat to find libraries that may hold this journal
Search WorldCat to find libraries that may hold this journal