Algebraic multigrid preconditioners for two-phase flow in porous media with phase transitions [Algebraic multigrid preconditioners for multiphase flow in porous media with phase transitions]
Abstract
Multiphase flow is a critical process in a wide range of applications, including oil and gas recovery, carbon sequestration, and contaminant remediation. Numerical simulation of multiphase flow requires solving of a large, sparse linear system resulting from the discretization of the partial differential equations modeling the flow. In the case of multiphase multicomponent flow with miscible effect, this is a very challenging task. The problem becomes even more difficult if phase transitions are taken into account. A new approach to handle phase transitions is to formulate the system as a nonlinear complementarity problem (NCP). Unlike in the primary variable switching technique, the set of primary variables in this approach is fixed even when there is phase transition. Not only does this improve the robustness of the nonlinear solver, it opens up the possibility to use multigrid methods to solve the resulting linear system. The disadvantage of the complementarity approach, however, is that when a phase disappears, the linear system has the structure of a saddle point problem and becomes indefinite, and current algebraic multigrid (AMG) algorithms cannot be applied directly. In this study, we explore the effectiveness of a new multilevel strategy, based on the multigrid reduction technique, to dealmore »
- Authors:
-
- Univ. of Maryland, College Park, MD (United States)
- Lawrence Livermore National Lab. (LLNL), Livermore, CA (United States)
- Publication Date:
- Research Org.:
- Lawrence Livermore National Laboratory (LLNL), Livermore, CA (United States)
- Sponsoring Org.:
- USDOE
- OSTI Identifier:
- 1438746
- Alternate Identifier(s):
- OSTI ID: 2325525
- Report Number(s):
- LLNL-JRNL-734458
Journal ID: ISSN 0309-1708
- Grant/Contract Number:
- AC52-07NA27344
- Resource Type:
- Accepted Manuscript
- Journal Name:
- Advances in Water Resources
- Additional Journal Information:
- Journal Volume: 114; Journal Issue: C; Journal ID: ISSN 0309-1708
- Publisher:
- Elsevier
- Country of Publication:
- United States
- Language:
- English
- Subject:
- 58 GEOSCIENCES; 02 PETROLEUM; 97 MATHEMATICS, COMPUTING, AND INFORMATION SCIENCE; Algebraic multigrid; Preconditioning; Compositional two-phase flow; Phase transitions; Nonlinear complementarity problem
Citation Formats
Bui, Quan M., Wang, Lu, and Osei-Kuffuor, Daniel. Algebraic multigrid preconditioners for two-phase flow in porous media with phase transitions [Algebraic multigrid preconditioners for multiphase flow in porous media with phase transitions]. United States: N. p., 2018.
Web. doi:10.1016/j.advwatres.2018.01.027.
Bui, Quan M., Wang, Lu, & Osei-Kuffuor, Daniel. Algebraic multigrid preconditioners for two-phase flow in porous media with phase transitions [Algebraic multigrid preconditioners for multiphase flow in porous media with phase transitions]. United States. https://doi.org/10.1016/j.advwatres.2018.01.027
Bui, Quan M., Wang, Lu, and Osei-Kuffuor, Daniel. Tue .
"Algebraic multigrid preconditioners for two-phase flow in porous media with phase transitions [Algebraic multigrid preconditioners for multiphase flow in porous media with phase transitions]". United States. https://doi.org/10.1016/j.advwatres.2018.01.027. https://www.osti.gov/servlets/purl/1438746.
@article{osti_1438746,
title = {Algebraic multigrid preconditioners for two-phase flow in porous media with phase transitions [Algebraic multigrid preconditioners for multiphase flow in porous media with phase transitions]},
author = {Bui, Quan M. and Wang, Lu and Osei-Kuffuor, Daniel},
abstractNote = {Multiphase flow is a critical process in a wide range of applications, including oil and gas recovery, carbon sequestration, and contaminant remediation. Numerical simulation of multiphase flow requires solving of a large, sparse linear system resulting from the discretization of the partial differential equations modeling the flow. In the case of multiphase multicomponent flow with miscible effect, this is a very challenging task. The problem becomes even more difficult if phase transitions are taken into account. A new approach to handle phase transitions is to formulate the system as a nonlinear complementarity problem (NCP). Unlike in the primary variable switching technique, the set of primary variables in this approach is fixed even when there is phase transition. Not only does this improve the robustness of the nonlinear solver, it opens up the possibility to use multigrid methods to solve the resulting linear system. The disadvantage of the complementarity approach, however, is that when a phase disappears, the linear system has the structure of a saddle point problem and becomes indefinite, and current algebraic multigrid (AMG) algorithms cannot be applied directly. In this study, we explore the effectiveness of a new multilevel strategy, based on the multigrid reduction technique, to deal with problems of this type. We demonstrate the effectiveness of the method through numerical results for the case of two-phase, two-component flow with phase appearance/disappearance. In conclusion, we also show that the strategy is efficient and scales optimally with problem size.},
doi = {10.1016/j.advwatres.2018.01.027},
journal = {Advances in Water Resources},
number = C,
volume = 114,
place = {United States},
year = {Tue Feb 06 00:00:00 EST 2018},
month = {Tue Feb 06 00:00:00 EST 2018}
}
Web of Science
Figures / Tables:
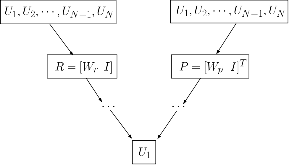 Fig. 1: Multigrid reduction V-cycle
Fig. 1: Multigrid reduction V-cycle
Works referenced in this record:
Method of Negative Saturations for Modeling Two-phase Compositional Flow with Oversaturated Zones
journal, December 2008
- Abadpour, Anahita; Panfilov, Mikhail
- Transport in Porous Media, Vol. 79, Issue 2
The Incomplete Factorization Multigraph Algorithm
journal, January 1999
- Bank, Randolph E.; Smith, R. Kent
- SIAM Journal on Scientific Computing, Vol. 20, Issue 4
Gas phase appearance and disappearance as a problem with complementarity constraints
journal, May 2014
- Ben Gharbia, Ibtihel; Jaffré, Jérôme
- Mathematics and Computers in Simulation, Vol. 99
Two-phase, partially miscible flow and transport modeling in porous media; application to gas migration in a nuclear waste repository
journal, August 2008
- Bourgeat, Alain; Jurak, Mladen; Smaï, Farid
- Computational Geosciences, Vol. 13, Issue 1
Algebraic Multigrid Preconditioners for Multiphase Flow in Porous Media
journal, January 2017
- Bui, Quan M.; Elman, Howard C.; Moulton, J. David
- SIAM Journal on Scientific Computing, Vol. 39, Issue 5
Multilevel block factorizations in generalized hierarchical bases
journal, January 2002
- Chow, Edmond; Vassilevski, Panayot S.
- Numerical Linear Algebra with Applications, Vol. 10, Issue 1-2
Constrained pressure residual multiscale (CPR-MS) method for fully implicit simulation of multiphase flow in porous media
journal, October 2015
- Cusini, Matteo; Lukyanov, Alexander A.; Natvig, Jostein
- Journal of Computational Physics, Vol. 299
Block Preconditioners Based on Approximate Commutators
journal, January 2006
- Elman, Howard; Howle, Victoria E.; Shadid, John
- SIAM Journal on Scientific Computing, Vol. 27, Issue 5
A taxonomy and comparison of parallel block multi-level preconditioners for the incompressible Navier–Stokes equations
journal, January 2008
- Elman, Howard; Howle, V. E.; Shadid, John
- Journal of Computational Physics, Vol. 227, Issue 3
Parallel Time Integration with Multigrid
journal, January 2014
- Falgout, R. D.; Friedhoff, S.; Kolev, Tz. V.
- SIAM Journal on Scientific Computing, Vol. 36, Issue 6
hypre: A Library of High Performance Preconditioners
book, April 2002
- Falgout, Robert D.; Yang, Ulrike Meier; Goos, Gerhard
- Computational Science — ICCS 2002: International Conference Amsterdam, The Netherlands, April 21–24, 2002 Proceedings, Part III
A generalized Block FSAI preconditioner for nonsymmetric linear systems
journal, January 2014
- Ferronato, Massimiliano; Janna, Carlo; Pini, Giorgio
- Journal of Computational and Applied Mathematics, Vol. 256
Robust numerical methods for saturated-unsaturated flow with dry initial conditions in heterogeneous media
journal, January 1995
- Forsyth, P. A.; Wu, Y. S.; Pruess, K.
- Advances in Water Resources, Vol. 18, Issue 1
BoomerAMG: A parallel algebraic multigrid solver and preconditioner
journal, April 2002
- Henson, Van Emden; Yang, Ulrike Meier
- Applied Numerical Mathematics, Vol. 41, Issue 1
The Primal-Dual Active Set Strategy as a Semismooth Newton Method
journal, January 2002
- Hintermüller, M.; Ito, K.; Kunisch, K.
- SIAM Journal on Optimization, Vol. 13, Issue 3
ILU Preconditioners for Nonsymmetric Saddle-Point Matrices with Application to the Incompressible Navier--Stokes Equations
journal, January 2015
- Konshin, Igor N.; Olshanskii, Maxim A.; Vassilevski, Yuri V.
- SIAM Journal on Scientific Computing, Vol. 37, Issue 5
A new approach for phase transitions in miscible multi-phase flow in porous media
journal, August 2011
- Lauser, A.; Hager, C.; Helmig, R.
- Advances in Water Resources, Vol. 34, Issue 8
Results of the MoMaS benchmark for gas phase appearance and disappearance using generalized MHFE
journal, November 2014
- Marchand, E.; Knabner, P.
- Advances in Water Resources, Vol. 73
Fully coupled generalised hybrid-mixed finite element approximation of two-phase two-component flow in porous media. Part II: numerical scheme and numerical results
journal, February 2012
- Marchand, Estelle; Müller, Torsten; Knabner, Peter
- Computational Geosciences, Vol. 16, Issue 3
Modeling and simulation of two-phase two-component flow with disappearing nonwetting phase
journal, October 2012
- Neumann, Rebecca; Bastian, Peter; Ippisch, Olaf
- Computational Geosciences, Vol. 17, Issue 1
Analytical decoupling techniques for fully implicit reservoir simulation
journal, May 2017
- Qiao, Changhe; Wu, Shuhong; Xu, Jinchao
- Journal of Computational Physics, Vol. 336
On the Approximate Cyclic Reduction Preconditioner
journal, January 1999
- Reusken, Arnold
- SIAM Journal on Scientific Computing, Vol. 21, Issue 2
A note on MGR methods
journal, February 1983
- Ries, Manfred; Trottenberg, Ulrich; Winter, Gerd
- Linear Algebra and its Applications, Vol. 49
A Preconditioned Iterative Method for Saddlepoint Problems
journal, July 1992
- Rusten, Torgeir; Winther, Ragnar
- SIAM Journal on Matrix Analysis and Applications, Vol. 13, Issue 3
GMRES: A Generalized Minimal Residual Algorithm for Solving Nonsymmetric Linear Systems
journal, July 1986
- Saad, Youcef; Schultz, Martin H.
- SIAM Journal on Scientific and Statistical Computing, Vol. 7, Issue 3
An algorithm for profile and wavefront reduction of sparse matrices
journal, February 1986
- Sloan, S. W.
- International Journal for Numerical Methods in Engineering, Vol. 23, Issue 2
A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils1
journal, January 1980
- van Genuchten, M. Th.
- Soil Science Society of America Journal, Vol. 44, Issue 5
Schur-complement multigrid
journal, February 1997
- Wagner, C.; Kinzelbach, W.; Wittum, G.
- Numerische Mathematik, Vol. 75, Issue 4
On the selection of primary variables in numerical formulation for modeling multiphase flow in porous media
journal, April 2001
- Wu, Yu-Shu; Forsyth, Peter A.
- Journal of Contaminant Hydrology, Vol. 48, Issue 3-4
A Multigrid Method Based on Incomplete Gaussian Elimination
journal, September 1996
- Reusken, Arnold
- Numerical Linear Algebra with Applications, Vol. 3, Issue 5
Results of the MoMaS benchmark for gas phase appearance and disappearance using generalized MHFE
journal, November 2014
- Marchand, E.; Knabner, P.
- Advances in Water Resources, Vol. 73
A Preconditioned Iterative Method for Saddlepoint Problems
journal, July 1992
- Rusten, Torgeir; Winther, Ragnar
- SIAM Journal on Matrix Analysis and Applications, Vol. 13, Issue 3
Figures / Tables found in this record:

 Search WorldCat to find libraries that may hold this journal
Search WorldCat to find libraries that may hold this journal