Skip to main content
OSTI.GOVU.S. Department of Energy Office of Scientific and Technical Information
U.S. Department of Energy
Office of Scientific and Technical Information
 

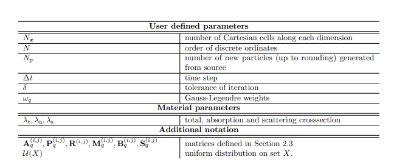
A hybrid Monte Carlo, discontinuous Galerkin method for linear kinetic transport equations

Journal Article · · Journal of Computational Physics
 [1];  [2];  [3]
  1. Univ. of Tennessee, Knoxville, TN (United States)
  2. Oak Ridge National Laboratory (ORNL), Oak Ridge, TN (United States)
  3. University of Notre Dame, IN (United States)
+ Show Author Affiliations

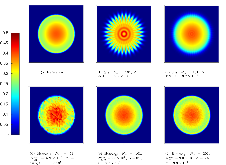
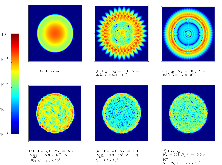
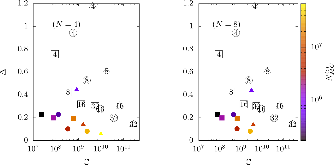
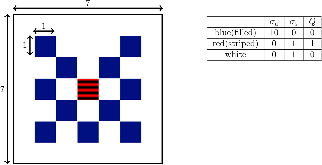
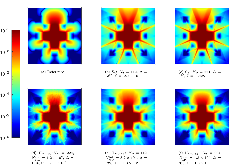
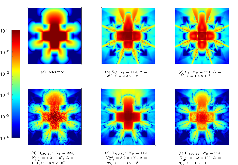
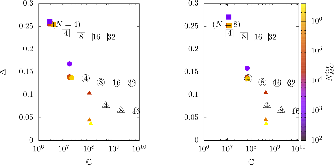
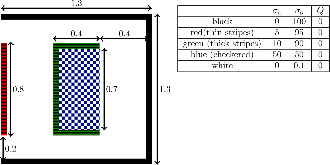
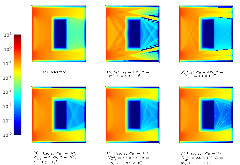
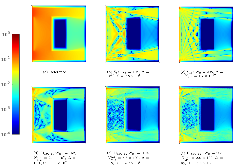
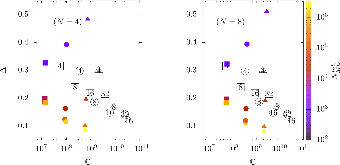
Here we present a hybrid method for time-dependent particle transport problems that combines Monte Carlo (MC) estimation with deterministic solutions based on discrete ordinates. For spatial discretizations, the MC algorithm computes a piecewise constant solution and the discrete ordinates use bilinear discontinuous finite elements. From the hybridization of the problem, the resulting problem solved by Monte Carlo is scattering free, resulting in a simple, efficient solution procedure. Between time steps, we use a projection approach to “relabel” collided particles as uncollided particles. In conclusion, from a series of standard 2-D Cartesian test problems we observe that our hybrid method has improved accuracy and reduction in computational complexity of approximately an order of magnitude relative to standard discrete ordinates solutions.

Research Organization:
Oak Ridge National Laboratory (ORNL), Oak Ridge, TN (United States)
Sponsoring Organization:
USDOE
Grant/Contract Number:
AC05-00OR22725
OSTI ID:
2538459
Journal Information:
Journal of Computational Physics, Journal Name: Journal of Computational Physics Vol. 514; ISSN 0021-9991
Publisher:
ElsevierCopyright Statement
Country of Publication:
United States
Language:
English

References (25)

Asymptotic solutions of numerical transport problems in optically thick, diffusive regimes journal April 1987
Asymptotic equilibrium diffusion analysis of time-dependent Monte Carlo methods for grey radiative transfer journal September 2004
A hybrid transport-diffusion method for Monte Carlo radiative-transfer simulations journal March 2007
A modified implicit Monte Carlo method for time-dependent radiative transfer with adaptive material coupling journal September 2009
A hybrid (Monte Carlo/deterministic) approach for multi-dimensional radiation transport journal August 2011
An arbitrary-order, fully implicit, hybrid kinetic solver for linear radiative transport using integral deferred correction journal October 2017
Hybrid methods for radiation transport using diagonally implicit Runge–Kutta and space–time discontinuous Galerkin time integration journal January 2019
Improvements to a class of hybrid methods for radiation transport: Nyström reconstruction and defect correction methods journal December 2020
A high-order/low-order (HOLO) algorithm for preserving conservation in time-dependent low-rank transport calculations journal December 2021
Multi-frequency implicit semi-analog Monte-Carlo (ISMC) radiative transfer solver in two-dimensions (without teleportation) journal February 2022
Review of Hybrid Methods for Deep-Penetration Neutron Transport journal April 2019
Multigroup Neutron Transport Using a Collision-Based Hybrid Method journal February 2023
A Comparison of Moment Closures for Linear Kinetic Transport Equations: The Line Source Benchmark journal September 2013
Moment-Based Acceleration of Monte Carlo Solution for Multifrequency Thermal Radiative Transfer Problems journal October 2014
The Incident Flux Response Expansion Method for Heterogeneous Coarse Mesh Transport Problems journal July 2006
Four Decades of Implicit Monte Carlo journal September 2015
A Continuous Source Tilting Scheme for Radiative Transfer Equations in Implicit Monte Carlo journal September 2020
Uniform convergence of an upwind discontinuous Galerkin method for solving scaled discrete-ordinate radiative transfer equations with isotropic scattering journal July 2021
Asymptotic Analysis of Upwind Discontinuous Galerkin Approximation of the Radiative Transport Equation in the Diffusive Limit journal January 2010
Discrete-Ordinate Discontinuous Galerkin Methods for Solving the Radiative Transfer Equation journal January 2010
A Collision-Based Hybrid Method for Time-Dependent, Linear, Kinetic Transport Equations journal January 2013
Discontinuous Finite Element Transport Solutions in Thick Diffusive Problems journal March 2001
A Hybrid Monte Carlo–Deterministic Method for Global Particle Transport Calculations journal February 2007
FW-CADIS Method for Global and Regional Variance Reduction of Monte Carlo Radiation Transport Calculations journal January 2014
Automated Variance Reduction of Monte Carlo Shielding Calculations Using the Discrete Ordinates Adjoint Function journal February 1998

Figures / Tables (12)

Table 1(p. 8)table Table 1
Figure 1(p. 13)figure Figure 1
Figure 2(p. 14)figure Figure 2
Figure 3(p. 15)figure Figure 3
Figure 4(p. 16)figure Figure 4
Figure 5(p. 16)figure Figure 5
Figure 6(p. 17)figure Figure 6
Figure 7(p. 18)figure Figure 7
Figure 8(p. 19)figure Figure 8
Figure 9(p. 20)figure Figure 9
Figure 10(p. 21)figure Figure 10
Figure 11(p. 22)figure Figure 11

Similar Records

Use of Monte Carlo procedures to estimate first and second collision sources for discrete ordinates transport codes
Journal Article · Thu Jul 01 00:00:00 EDT 1993 · Nuclear Science and Engineering; (United States) · OSTI ID:6326046
A Hybrid Finite-Volume, Discontinuous Galerkin Discretization for the Radiative Transport Equation
Journal Article · Wed Jan 06 23:00:00 EST 2021 · Multiscale Modeling & Simulation · OSTI ID:1846554
A Hybrid Monte Carlo-Deterministic Method for Global Binary Stochastic Medium Transport Problems
Conference · Wed Mar 03 23:00:00 EST 2010 · OSTI ID:992298

Related Subjects

97 MATHEMATICS AND COMPUTING
Hybrid stochastic-deterministic method
Kinetic equations
Monte Carlo
Particle transport