tLaSDI: Thermodynamics-informed latent space dynamics identification

Park, Jun Sur Richard; Cheung, Siu Wun; Choi, Youngsoo; Shin, Yeonjong

doi:10.1016/j.cma.2024.117144

tLaSDI: Thermodynamics-informed latent space dynamics identification

Journal Article · Mon Jul 01 00:00:00 EDT 2024 · Computer Methods in Applied Mechanics and Engineering

DOI:https://doi.org/10.1016/j.cma.2024.117144· OSTI ID:2429372

Park, Jun Sur Richard ^[1]; ^[2]; ^[2]; ^[3]

Korea Institute for Advanced Study (KIAS), Seoul (Korea, Republic of)
Lawrence Livermore National Laboratory (LLNL), Livermore, CA (United States)
North Carolina State University, Raleigh, NC (United States); Pohang Univ. of Science and Technology (POSTECH) (Korea, Republic of)

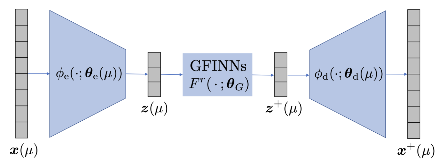
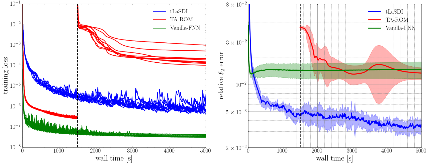
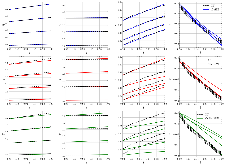
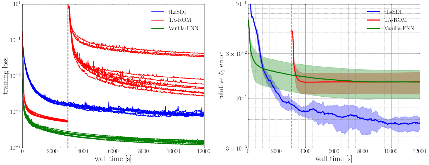
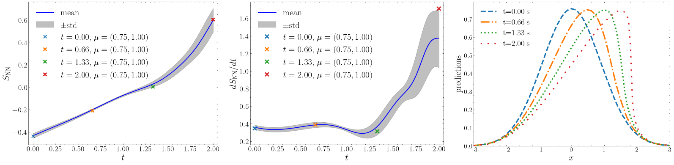
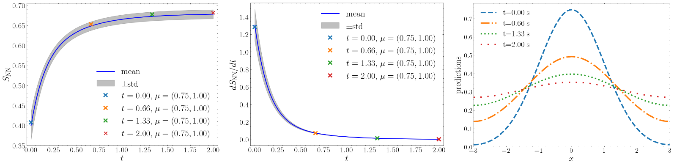
Here we propose a latent space dynamics identification method, namely tLaSDI, that embeds the first and second principles of thermodynamics. The latent variables are learned through an autoencoder as a nonlinear dimension reduction model. The latent dynamics are constructed by a neural network-based model that precisely preserves certain structures for the thermodynamic laws through the GENERIC formalism. An abstract error estimate is established, which provides a new loss formulation involving the Jacobian computation of autoencoder. The autoencoder and the latent dynamics are simultaneously trained to minimize the new loss. Computational examples demonstrate the effectiveness of tLaSDI, which exhibits robust generalization ability, even in extrapolation. In addition, an intriguing correlation is empirically observed between a quantity from tLaSDI in the latent space and the behaviors of the full-state solution.

View Accepted Manuscript (DOE)

Research Organization:: Lawrence Livermore National Laboratory (LLNL), Livermore, CA (United States)

Sponsoring Organization:: USDOE National Nuclear Security Administration (NNSA); USDOE Laboratory Directed Research and Development (LDRD) Program; USDOE Office of Science (SC), Advanced Scientific Computing Research (ASCR)

Grant/Contract Number:: AC52-07NA27344; SC0023164

OSTI ID:: 2429372

Report Number(s):: LLNL--JRNL-860848; 1092545

Journal Information:: Computer Methods in Applied Mechanics and Engineering, Journal Name: Computer Methods in Applied Mechanics and Engineering Vol. 429; ISSN 0045-7825

Publisher:: ElsevierCopyright Statement

Country of Publication:: United States

Language:: English

References (38)

Approximation by superpositions of a sigmoidal function Cybenko, G. Mathematics of Control, Signals, and Systems, Vol. 2, Issue 4 https://doi.org/10.1007/BF02551274	journal	December 1989
POD and CVT-based reduced-order modeling of Navier–Stokes flows Burkardt, John; Gunzburger, Max; Lee, Hyung-Chun Computer Methods in Applied Mechanics and Engineering, Vol. 196, Issue 1-3 https://doi.org/10.1016/j.cma.2006.04.004	journal	December 2006
Deep learning of thermodynamics-aware reduced-order models from data Hernandez, Quercus; Badías, Alberto; González, David Computer Methods in Applied Mechanics and Engineering, Vol. 379 https://doi.org/10.1016/j.cma.2021.113763	journal	June 2021
Reduced order models for Lagrangian hydrodynamics Copeland, Dylan Matthew; Cheung, Siu Wun; Huynh, Kevin Computer Methods in Applied Mechanics and Engineering, Vol. 388 https://doi.org/10.1016/j.cma.2021.114259	journal	January 2022
Multiscale modeling of inelastic materials with Thermodynamics-based Artificial Neural Networks (TANN) Masi, Filippo; Stefanou, Ioannis Computer Methods in Applied Mechanics and Engineering, Vol. 398 https://doi.org/10.1016/j.cma.2022.115190	journal	August 2022
LaSDI: Parametric Latent Space Dynamics Identification Fries, William D.; He, Xiaolong; Choi, Youngsoo Computer Methods in Applied Mechanics and Engineering, Vol. 399 https://doi.org/10.1016/j.cma.2022.115436	journal	September 2022
Reduced order modeling of parametrized systems through autoencoders and SINDy approach: continuation of periodic solutions Conti, Paolo; Gobat, Giorgio; Fresca, Stefania Computer Methods in Applied Mechanics and Engineering, Vol. 411 https://doi.org/10.1016/j.cma.2023.116072	journal	June 2023
GPLaSDI: Gaussian Process-based interpretable Latent Space Dynamics Identification through deep autoencoder Bonneville, Christophe; Choi, Youngsoo; Ghosh, Debojyoti Computer Methods in Applied Mechanics and Engineering, Vol. 418 https://doi.org/10.1016/j.cma.2023.116535	journal	January 2024
POD/DEIM nonlinear model order reduction of an ADI implicit shallow water equations model Ştefănescu, R.; Navon, I. M. Journal of Computational Physics, Vol. 237 https://doi.org/10.1016/j.jcp.2012.11.035	journal	March 2013
Non-linear model reduction for the Navier–Stokes equations using residual DEIM method Xiao, D.; Fang, F.; Buchan, A. G. Journal of Computational Physics, Vol. 263 https://doi.org/10.1016/j.jcp.2014.01.011	journal	April 2014
Hidden physics models: Machine learning of nonlinear partial differential equations Raissi, Maziar; Karniadakis, George Em Journal of Computational Physics, Vol. 357 https://doi.org/10.1016/j.jcp.2017.11.039	journal	March 2018
Conservative model reduction for finite-volume models Carlberg, Kevin; Choi, Youngsoo; Sargsyan, Syuzanna Journal of Computational Physics, Vol. 371 https://doi.org/10.1016/j.jcp.2018.05.019	journal	October 2018
Model reduction of dynamical systems on nonlinear manifolds using deep convolutional autoencoders Lee, Kookjin; Carlberg, Kevin T. Journal of Computational Physics https://doi.org/10.1016/j.jcp.2019.108973	journal	November 2019
Data-driven deep learning of partial differential equations in modal space Wu, Kailiang; Xiu, Dongbin Journal of Computational Physics, Vol. 408 https://doi.org/10.1016/j.jcp.2020.109307	journal	May 2020
Space–time reduced order model for large-scale linear dynamical systems with application to Boltzmann transport problems Choi, Youngsoo; Brown, Peter; Arrighi, William Journal of Computational Physics, Vol. 424 https://doi.org/10.1016/j.jcp.2020.109845	journal	January 2021
Structure-preserving neural networks Hernández, Quercus; Badías, Alberto; González, David Journal of Computational Physics, Vol. 426 https://doi.org/10.1016/j.jcp.2020.109950	journal	February 2021
A fast and accurate physics-informed neural network reduced order model with shallow masked autoencoder Kim, Youngkyu; Choi, Youngsoo; Widemann, David Journal of Computational Physics, Vol. 451 https://doi.org/10.1016/j.jcp.2021.110841	journal	February 2022
Local Lagrangian reduced-order modeling for the Rayleigh-Taylor instability by solution manifold decomposition Cheung, Siu Wun; Choi, Youngsoo; Copeland, Dylan Matthew Journal of Computational Physics, Vol. 472 https://doi.org/10.1016/j.jcp.2022.111655	journal	January 2023
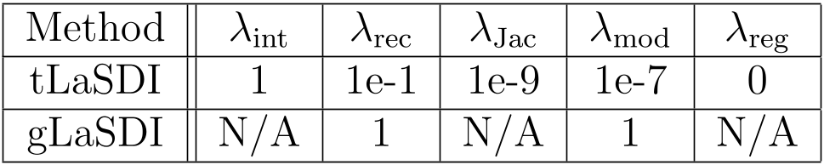
gLaSDI: Parametric physics-informed greedy latent space dynamics identification He, Xiaolong; Choi, Youngsoo; Fries, William D. Journal of Computational Physics, Vol. 489 https://doi.org/10.1016/j.jcp.2023.112267	journal	September 2023
Approximation rates for neural networks with general activation functions Siegel, Jonathan W.; Xu, Jinchao Neural Networks, Vol. 128 https://doi.org/10.1016/j.neunet.2020.05.019	journal	August 2020
Dynamic mode decomposition of numerical and experimental data Schmid, Peter J. Journal of Fluid Mechanics, Vol. 656 https://doi.org/10.1017/S0022112010001217	journal	July 2010
SciPy 1.0: fundamental algorithms for scientific computing in Python Virtanen, Pauli; Gommers, Ralf; Oliphant, Travis E. Nature Methods https://doi.org/10.1038/s41592-019-0686-2	journal	February 2020
Automated reverse engineering of nonlinear dynamical systems Bongard, J.; Lipson, H. Proceedings of the National Academy of Sciences, Vol. 104, Issue 24 https://doi.org/10.1073/pnas.0609476104	journal	June 2007
Discovering governing equations from data by sparse identification of nonlinear dynamical systems Brunton, Steven L.; Proctor, Joshua L.; Kutz, J. Nathan Proceedings of the National Academy of Sciences, Vol. 113, Issue 15 https://doi.org/10.1073/pnas.1517384113	journal	March 2016
Data-driven discovery of coordinates and governing equations Champion, Kathleen; Lusch, Bethany; Kutz, J. Nathan Proceedings of the National Academy of Sciences, Vol. 116, Issue 45 https://doi.org/10.1073/pnas.1906995116	journal	October 2019
Structure-preserving integrators for dissipative systems based on reversible– irreversible splitting Shang, Xiaocheng; Öttinger, Hans Christian Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, Vol. 476, Issue 2234 https://doi.org/10.1098/rspa.2019.0446	journal	February 2020
GFINNs: GENERIC formalism informed neural networks for deterministic and stochastic dynamical systems Zhang, Zhen; Shin, Yeonjong; Em Karniadakis, George Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, Vol. 380, Issue 2229 https://doi.org/10.1098/rsta.2021.0207	journal	June 2022
Dynamics and thermodynamics of complex fluids. I. Development of a general formalism Grmela, Miroslav; Öttinger, Hans Christian Physical Review E, Vol. 56, Issue 6 https://doi.org/10.1103/PhysRevE.56.6620	journal	December 1997
Dynamics and thermodynamics of complex fluids. II. Illustrations of a general formalism Öttinger, Hans Christian; Grmela, Miroslav Physical Review E, Vol. 56, Issue 6 https://doi.org/10.1103/PhysRevE.56.6633	journal	December 1997
Preservation of thermodynamic structure in model reduction Öttinger, Hans Christian Physical Review E, Vol. 91, Issue 3 https://doi.org/10.1103/PhysRevE.91.032147	journal	March 2015
OnsagerNet: Learning stable and interpretable dynamics using a generalized Onsager principle Yu, Haijun; Tian, Xinyuan; E., Weinan Physical Review Fluids, Vol. 6, Issue 11 https://doi.org/10.1103/PhysRevFluids.6.114402	journal	November 2021
Physics Perception in Sloshing Scenes With Guaranteed Thermodynamic Consistency Moya, Beatriz; Badias, Alberto; Gonzalez, David IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 45, Issue 2 https://doi.org/10.1109/TPAMI.2022.3160100	journal	February 2023
Reducing the Dimensionality of Data with Neural Networks Hinton, G. E. Science, Vol. 313, Issue 5786 https://doi.org/10.1126/science.1127647	journal	July 2006
Distilling Free-Form Natural Laws from Experimental Data Schmidt, Michael; Lipson, Hod Science, Vol. 324, Issue 5923 https://doi.org/10.1126/science.1165893	journal	April 2009
Space--Time Least-Squares Petrov--Galerkin Projection for Nonlinear Model Reduction Choi, Youngsoo; Carlberg, Kevin SIAM Journal on Scientific Computing, Vol. 41, Issue 1 https://doi.org/10.1137/17M1120531	journal	January 2019
SNS: A Solution-Based Nonlinear Subspace Method for Time-Dependent Model Order Reduction Choi, Youngsoo; Coombs, Deshawn; Anderson, Robert SIAM Journal on Scientific Computing, Vol. 42, Issue 2 https://doi.org/10.1137/19M1242963	journal	January 2020
POD-DEIM Based Model Order Reduction for the Spherical Shallow Water Equations with Turkel-Zwas Finite Difference Discretization Zhao, Pengfei; Liu, Cai; Feng, Xuan Journal of Applied Mathematics, Vol. 2014 https://doi.org/10.1155/2014/292489	journal	January 2014
Neural Networks for Optimal Approximation of Smooth and Analytic Functions Mhaskar, H. N. Neural Computation, Vol. 8, Issue 1 https://doi.org/10.1162/neco.1996.8.1.164	journal	January 1996