Skip to main content
OSTI.GOVU.S. Department of Energy Office of Scientific and Technical Information
U.S. Department of Energy
Office of Scientific and Technical Information
 

Multigrid Reduction in Time for Chaotic Dynamical Systems

Journal Article · · SIAM Journal on Scientific Computing
DOI:https://doi.org/10.1137/22m1518335· OSTI ID:2212873
 [1];  [2];  [2];  [1]
  1. Univ. of New Mexico, Albuquerque, NM (United States)
  2. Lawrence Livermore National Laboratory (LLNL), Livermore, CA (United States)
+ Show Author Affiliations

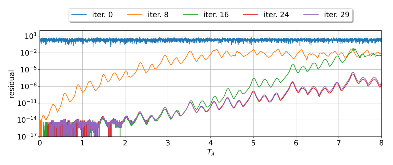
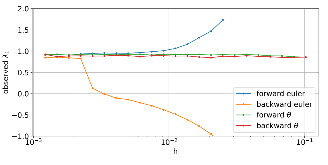
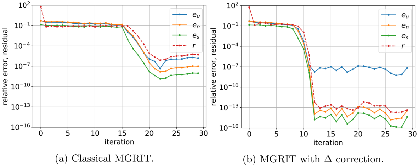
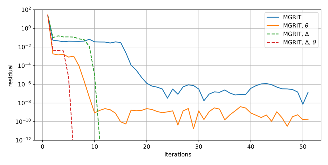
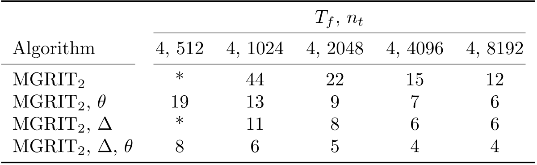
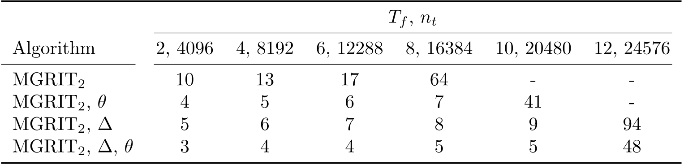
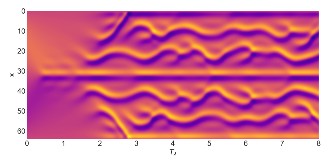
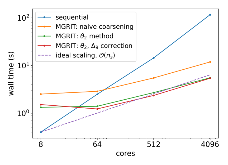
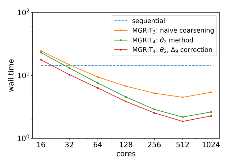
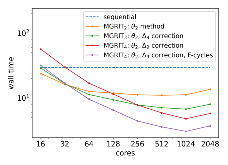
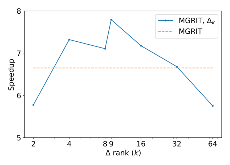
As CPU clock speeds have stagnated and high performance computers continue to have ever higher core counts, increased parallelism is needed to take advantage of these new architectures. Traditional serial time-marching schemes can be a significant bottleneck, as many types of simulations require large numbers of time-steps which must be computed sequentially. Parallel-in-time schemes, such as the Multigrid Reduction in Time (MGRIT) method, remedy this by parallelizing across time-steps and have shown promising results for parabolic problems. However, chaotic problems have proved more difficult, since chaotic initial value problems (IVPs) are inherently ill-conditioned. MGRIT relies on a hierarchy of successively coarser time-grids to iteratively correct the solution on the finest time-grid, but due to the nature of chaotic systems, small inaccuracies on the coarser levels can be greatly magnified and lead to poor coarse-grid corrections. Here we introduce a modified MGRIT algorithm based on an existing quadratically converging nonlinear extension to the multigrid Full Approximation Scheme (FAS), as well as a novel time-coarsening scheme. Together, these approaches better capture long-term chaotic behavior on coarse-grids and greatly improve convergence of MGRIT for chaotic IVPs. Further, we introduce a novel low-memory variant of the algorithm for solving chaotic PDEs with MGRIT which not only solves the IVP, but also provides estimates for the unstable Lyapunov vectors of the system. Finally, we provide supporting numerical results for the Lorenz system and demonstrate parallel speedup for the chaotic Kuramoto–Sivashinsky PDE over a significantly longer time-domain than in previous works.

Research Organization:
Lawrence Livermore National Laboratory (LLNL), Livermore, CA (United States)
Sponsoring Organization:
USDOE National Nuclear Security Administration (NNSA)
Grant/Contract Number:
AC52-07NA27344
OSTI ID:
2212873
Report Number(s):
LLNL--JRNL-838414; 1058785
Journal Information:
SIAM Journal on Scientific Computing, Journal Name: SIAM Journal on Scientific Computing Journal Issue: 4 Vol. 45; ISSN 1064-8275
Publisher:
Society for Industrial and Applied Mathematics (SIAM)Copyright Statement
Country of Publication:
United States
Language:
English

References (22)

Optimizing multigrid reduction‐in‐time and Parareal coarse‐grid operators for linear advection journal March 2021
50 Years of Time Parallel Time Integration book January 2015
Nonlinear Convergence Analysis for the Parareal Algorithm book January 2008
Theory and Computation of Covariant Lyapunov Vectors journal March 2012
Multigrid methods with space–time concurrency journal August 2017
Applications of time parallelization journal September 2020
Performance of parallel-in-time integration for Rayleigh Bénard convection journal September 2020
What good are numerical simulations of chaotic dynamical systems? journal November 1994
Parallelization in time of numerical simulations of fully-developed plasma turbulence using the parareal algorithm journal September 2010
The drag-adjoint field of a circular cylinder wake at Reynolds numbers 20, 100 and 500 journal July 2013
Towards scalable parallel-in-time turbulent flow simulations journal November 2013
Multi-level adaptive solutions to boundary-value problems journal May 1977
A Multilevel Nonlinear Method journal January 2006
Analysis of the Parareal Time‐Parallel Time‐Integration Method journal January 2007
Parallel Time Integration with Multigrid journal January 2014
Two-Level Convergence Theory for Multigrid Reduction in Time (MGRIT) journal January 2017
Coarse-Grid Correction for Nonelliptic and Singular Perturbation Problems journal September 1998
Diffusion-Induced Chaos in Reaction Systems journal January 1978
Parallel methods for integrating ordinary differential equations journal December 1964
Algorithm 832: UMFPACK V4.3---an unsymmetric-pattern multifrontal method journal June 2004
Toward an efficient parallel in time method for partial differential equations journal January 2012
Irregularity: a fundamentd property of the atmosphere journal January 1984

Figures / Tables (13)

Fig. 1(p. 6)figure Fig. 1
Fig. 2(p. 10)figure Fig. 2
Fig. 3(p. 10)figure Fig. 3
Fig. 4(p. 14)figure Fig. 4
Fig. 5(p. 19)figure Fig. 5
Table 1(p. 19)table Table 1
Table 2(p. 20)table Table 2
Table 3(p. 21)table Table 3
Fig. 6(p. 22)figure Fig. 6
Fig. 7(p. 23)figure Fig. 7
Fig. 8(p. 24)figure Fig. 8
Fig. 10(p. 25)figure Fig. 10
Fig. 9(p. 25)figure Fig. 9

Similar Records

Two-Level Convergence Theory for Multigrid Reduction in Time (MGRIT)
Journal Article · Thu Oct 26 00:00:00 EDT 2017 · SIAM Journal on Scientific Computing · OSTI ID:1764758
Fast Multigrid Reduction-in-Time for Advection via Modified Semi-Lagrangian Coarse-Grid Operators
Journal Article · Mon Jul 24 00:00:00 EDT 2023 · SIAM Journal on Scientific Computing · OSTI ID:1995057
Efficient Multigrid Reduction-in-Time for Method-of-Lines Discretizations of Linear Advection
Journal Article · Wed May 17 00:00:00 EDT 2023 · Journal of Scientific Computing · OSTI ID:1985223

Related Subjects

97 MATHEMATICS AND COMPUTING
Lorenz system
Lyapunov vectors
chaotic problems
multigrid
multigrid in reduction time
parallel-in-time