Fast computation of synthetic seismograms within a medium containing remote localized perturbations: a numerical solution to the scattering problem

Masson, Yder; Romanowicz, Barbara

doi:10.1093/gji/ggw412

Fast computation of synthetic seismograms within a medium containing remote localized perturbations: a numerical solution to the scattering problem

Journal Article · Fri Nov 04 00:00:00 EDT 2016 · Geophysical Journal International

DOI:https://doi.org/10.1093/gji/ggw412· OSTI ID:1526206

Masson, Yder ^[1]; Romanowicz, Barbara ^[2]

Inst. de Physique du Globe, Paris (France)
Inst. de Physique du Globe, Paris (France); College de France, Paris (France); Univ. of California, Berkeley, CA (United States). Berkeley Siesmological Laboratory

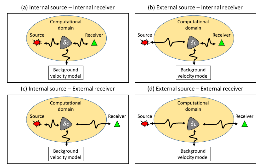
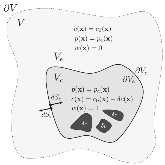
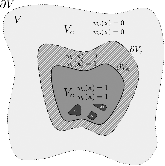
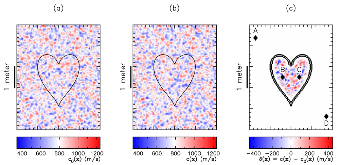
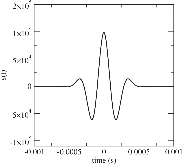
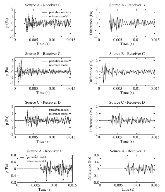
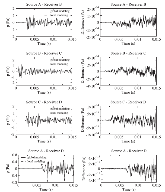
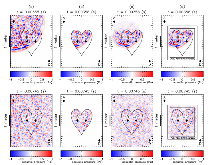
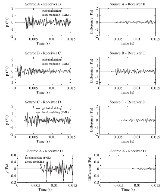
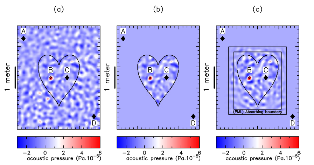
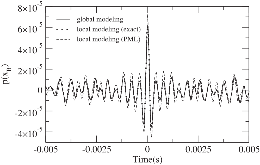
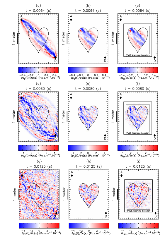
We derive a fast discrete solution to the scattering problem. This solution allows us to compute accurate synthetic seismograms or waveforms for arbitrary locations of sources and receivers within a medium containing localized perturbations. The key to efficiency is that wave propagation modelling does not need to be carried out in the entire volume that encompasses the sources and the receivers but only within the subvolume containing the perturbations or scatterers. The proposed solution has important applications, for example, it permits the imaging of remote targets located in regions where no sources or receivers are present. Our solution relies on domain decomposition: within a small volume that contains the scatterers, wave propagation is modelled numerically, while in the surrounding volume, where the medium isn't perturbed, the response is obtained through wavefield extrapolation. The originality of this work is the derivation of discrete formulas for representation theorems and Kirchhof–Helmholtz integrals that naturally adapt to the numerical scheme employed for modelling wave propagation. Our solution applies, for example, to finite difference methods or finite/spectral elements methods. The synthetic seismograms obtained with our solution can be considered ‘exact’ as the total numerical error is comparable to that of the method employed for modelling wave propagation. We detail a basic implementation of our solution in the acoustic case using the finite difference method and present numerical examples that demonstrate the accuracy of the method. We show that ignoring some terms accounting for higher order scattering effects in our solution has a limited effect on the computed seismograms and significantly reduces the computational effort. Finally, we show that our solution can be used to compute localized sensitivity kernels and we discuss applications to target oriented imaging. Extension to the elastic case is straightforward and summarized in a dedicated section.

View Accepted Manuscript (DOE)

Research Organization:: Lawrence Berkeley National Lab. (LBNL), Berkeley, CA (United States). National Energy Research Scientific Computing Center (NERSC)

Sponsoring Organization:: USDOE Office of Science (SC)

Grant/Contract Number:: AC02-05CH11231

OSTI ID:: 1526206

Journal Information:: Geophysical Journal International, Journal Name: Geophysical Journal International Journal Issue: 2 Vol. 208; ISSN 0956-540X

Publisher:: Oxford University PressCopyright Statement

Country of Publication:: United States

Language:: English

References (37)

On the effective seismic input for non-linear soil-structure interaction systems Bielak, Jacobo; Christiano, Paul Earthquake Engineering & Structural Dynamics, Vol. 12, Issue 1 https://doi.org/10.1002/eqe.4290120108	journal	January 1984
General Theory of Elastic Wave Scattering Snieder, Roel Scattering https://doi.org/10.1016/b978-012613760-6/50027-9	book	January 2002
Global approach for transient shear wave inversion based on the adjoint method: a comprehensive 2D simulation study Arnal, B.; Pinton, G.; Garapon, P. Physics in Medicine and Biology, Vol. 58, Issue 19 https://doi.org/10.1088/0031-9155/58/19/6765	journal	September 2013
A hybrid method to compute short-period synthetic seismograms of teleseismic body waves in a 3-D regional model Monteiller, Vadim; Chevrot, Sébastien; Komatitsch, Dimitri Geophysical Journal International, Vol. 192, Issue 1 https://doi.org/10.1093/gji/ggs006	journal	November 2012
On the numerical implementation of time-reversal mirrors for tomographic imaging Masson, Yder; Cupillard, Paul; Capdeville, Yann Geophysical Journal International, Vol. 196, Issue 3 https://doi.org/10.1093/gji/ggt459	journal	December 2013
Three-dimensional full waveform inversion of short-period teleseismic wavefields based upon the SEM–DSM hybrid method Monteiller, Vadim; Chevrot, Sébastien; Komatitsch, Dimitri Geophysical Journal International, Vol. 202, Issue 2 https://doi.org/10.1093/gji/ggv189	journal	May 2015
An efficient method of 3-D elastic full waveform inversion using a finite-difference injection method for time-lapse imaging Borisov, Dmitry; Singh, Satish C.; Fuji, Nobuaki Geophysical Journal International, Vol. 202, Issue 3 https://doi.org/10.1093/gji/ggv268	journal	July 2015
Adjoint Tomography of the Southern California Crust Tape, C.; Liu, Q.; Maggi, A. Science, Vol. 325, Issue 5943 https://doi.org/10.1126/science.1175298	journal	August 2009
Waveform Tomography Reveals Channeled Flow at the Base of the Oceanic Asthenosphere French, S.; Lekic, V.; Romanowicz, B. Science, Vol. 342, Issue 6155 https://doi.org/10.1126/science.1241514	journal	September 2013
Inversion of seismic reflection data in the acoustic approximation Tarantola, Albert GEOPHYSICS, Vol. 49, Issue 8 https://doi.org/10.1190/1.1441754	journal	August 1984
Domain Reduction Method for Three-Dimensional Earthquake Modeling in Localized Regions, Part I: Theory Bielak, J. Bulletin of the Seismological Society of America, Vol. 93, Issue 2 https://doi.org/10.1785/0120010251	journal	April 2003
A perfectly matched layer for the absorption of electromagnetic waves Berenger, Jean-Pierre Journal of Computational Physics, Vol. 114, Issue 2 https://doi.org/10.1006/jcph.1994.1159	journal	October 1994
Full Seismic Waveform Modelling and Inversion Fichtner, Andreas Advances in Geophysical and Environmental Mechanics and Mathematics https://doi.org/10.1007/978-3-642-15807-0	book	January 2011
General Theory of Elastic Wave Scattering Snieder, Roel Scattering https://doi.org/10.1016/B978-012613760-6/50027-9	book	January 2002
Boundary Integral Equations and Boundary Elements Methods in Elastodynamics Bouchon, Michel; Sánchez-Sesma, Francisco J. Advances in Wave Propagation in Heterogenous Earth https://doi.org/10.1016/S0065-2687(06)48003-1	book	January 2007
3D effects of sharp boundaries at the borders of the African and Pacific Superplumes: Observation and modeling To, A.; Romanowicz, B.; Capdeville, Y. Earth and Planetary Science Letters, Vol. 233, Issue 1-2 https://doi.org/10.1016/j.epsl.2005.01.037	journal	April 2005
Lithospheric expression of geological units in central and eastern North America from full waveform tomography Yuan, Huaiyu; French, Scott; Cupillard, Paul Earth and Planetary Science Letters, Vol. 402 https://doi.org/10.1016/j.epsl.2013.11.057	journal	September 2014
A two-dimensional hybrid method for modeling seismic wave propagation in anisotropic media Zhao, Liang; Wen, Lianxing; Chen, Ling Journal of Geophysical Research, Vol. 113, Issue B12 https://doi.org/10.1029/2008JB005733	journal	January 2008
A two-dimensional P-SV hybrid method and its application to modeling localized structures near the core-mantle boundary Wen, Lianxing; Helmberger, Donald V. Journal of Geophysical Research: Solid Earth, Vol. 103, Issue B8 https://doi.org/10.1029/98JB01276	journal	August 1998
Structure of the European upper mantle revealed by adjoint tomography Zhu, Hejun; Bozdağ, Ebru; Peter, Daniel Nature Geoscience, Vol. 5, Issue 7 https://doi.org/10.1038/ngeo1501	journal	June 2012
Coupling spectral elements and modes in a spherical Earth: an extension to the ‘sandwich’ case Capdeville, Y.; To, A.; Romanowicz, B. Geophysical Journal International, Vol. 154, Issue 1 https://doi.org/10.1046/j.1365-246X.2003.01959.x	journal	July 2003
Accurate numerical methods for solving the elastic equation of motion for arbitrary source locations Takeuchi, Nozomu; Geller, Robert J. Geophysical Journal International, Vol. 154, Issue 3 https://doi.org/10.1046/j.1365-246X.2003.02009.x	journal	September 2003
Multiscale full waveform inversion Fichtner, Andreas; Trampert, Jeannot; Cupillard, Paul Geophysical Journal International, Vol. 194, Issue 1 https://doi.org/10.1093/gji/ggt118	journal	April 2013
A numerically exact local solver applied to salt boundary inversion in seismic full-waveform inversion Willemsen, Bram; Malcolm, Alison; Lewis, Winston Geophysical Journal International, Vol. 204, Issue 3 https://doi.org/10.1093/gji/ggv547	journal	February 2016
Time reversal of ultrasonic fields. I. Basic principles Fink, M. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, Vol. 39, Issue 5 https://doi.org/10.1109/58.156174	journal	September 1992
Numerical Solution of Steady-State Electromagnetic Scattering Problems Using the Time-Dependent Maxwell's Equations Taflove, A.; Brodwin, M. E. IEEE Transactions on Microwave Theory and Techniques, Vol. 23, Issue 8 https://doi.org/10.1109/TMTT.1975.1128640	journal	August 1975
Seismic tomography, adjoint methods, time reversal and banana-doughnut kernels: Seismic tomography, adjoint methods, time reversal and banana-doughnut kernels Tromp, Jeroen; Tape, Carl; Liu, Qinya Geophysical Journal International, Vol. 160, Issue 1 https://doi.org/10.1111/j.1365-246X.2004.02453.x	journal	December 2004
The source-box wave propagation hybrid methods: general formulation and implementation Opršal, I.; Matyska, C.; Irikura, K. Geophysical Journal International, Vol. 176, Issue 2 https://doi.org/10.1111/j.1365-246X.2008.03986.x	journal	February 2009
Exact wave field simulation for finite-volume scattering problems van Manen, Dirk-Jan; Robertsson, Johan O. A.; Curtis, Andrew The Journal of the Acoustical Society of America, Vol. 122, Issue 4 https://doi.org/10.1121/1.2771371	journal	October 2007
Inversion of normal incidence seismograms Bamberger, A.; Chavent, G.; Hemon, Ch. GEOPHYSICS, Vol. 47, Issue 5 https://doi.org/10.1190/1.1441345	journal	May 1982
A finite‐difference injection approach to modeling seismic fluid flow monitoring Robertsson, Johan O. A.; Ryan‐Grigor, Sarah; Sayers, Colin M. GEOPHYSICS, Vol. 65, Issue 3 https://doi.org/10.1190/1.1444786	journal	May 2000
An efficient method for calculating finite‐difference seismograms after model alterations Robertsson, Johan O. A.; Chapman, Chris H. GEOPHYSICS, Vol. 65, Issue 3 https://doi.org/10.1190/1.1444787	journal	May 2000
An overview of full-waveform inversion in exploration geophysics Virieux, J.; Operto, S. GEOPHYSICS, Vol. 74, Issue 6 https://doi.org/10.1190/1.3238367	journal	November 2009
Domain Reduction Method for Three-Dimensional Earthquake Modeling in Localized Regions, Part II: Verification and Applications Yoshimura, C. Bulletin of the Seismological Society of America, Vol. 93, Issue 2 https://doi.org/10.1785/0120010252	journal	April 2003
Full 3D Tomography for the Crustal Structure of the Los Angeles Region Chen, P.; Zhao, L.; Jordan, T. H. Bulletin of the Seismological Society of America, Vol. 97, Issue 4 https://doi.org/10.1785/0120060222	journal	August 2007
Numerical Simulation of Ground Rotations along 2D Topographical Profiles under the Incidence of Elastic Plane Waves Godinho, L.; Amado Mendes, P.; Tadeu, A. Bulletin of the Seismological Society of America, Vol. 99, Issue 2B https://doi.org/10.1785/0120080096	journal	May 2009
Instaseis: instant global seismograms based on a broadband waveform database van Driel, M.; Krischer, L.; Stähler, S. C. Solid Earth, Vol. 6, Issue 2 https://doi.org/10.5194/se-6-701-2015	journal	January 2015

Cited By (2)

Enabling numerically exact local solver for waveform inversion—a low-rank approach Kumar, Rajiv; Willemsen, Bram; Herrmann, Felix J. Computational Geosciences, Vol. 23, Issue 4 https://doi.org/10.1007/s10596-019-09832-9	journal	June 2019
High-frequency seismic wave modelling of the deep Earth based on hybrid methods and spectral-element simulations: a conceptual study Lin, Chuangxin; Monteiller, Vadim; Wang, Kai Geophysical Journal International, Vol. 219, Issue 3 https://doi.org/10.1093/gji/ggz413	journal	September 2019