On ’t Hooft defects, monopole bubbling and supersymmetric quantum mechanics
- Rutgers Univ., Piscataway, NJ (United States). NHETC. Dept. of Physics and Astronomy
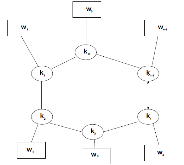
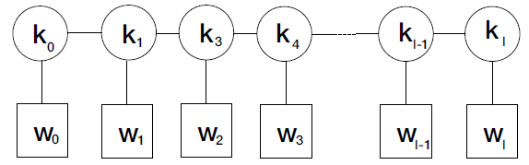
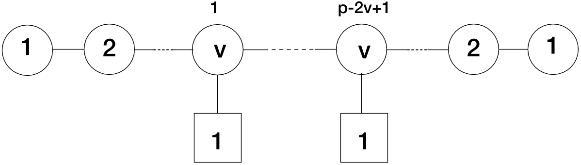
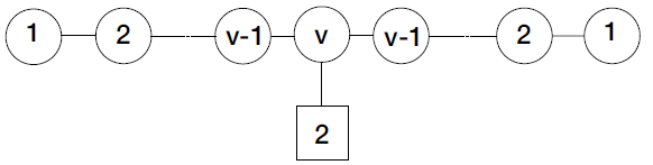
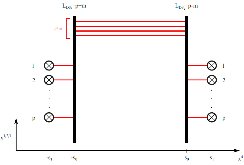
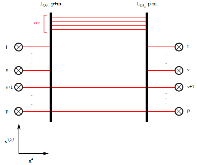
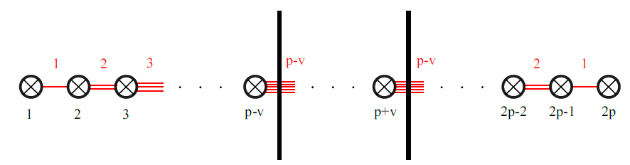
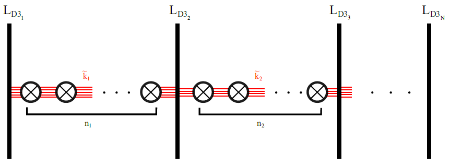
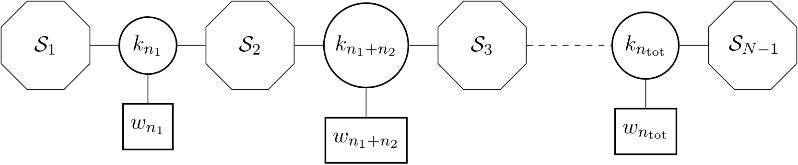
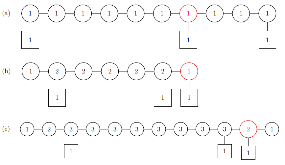
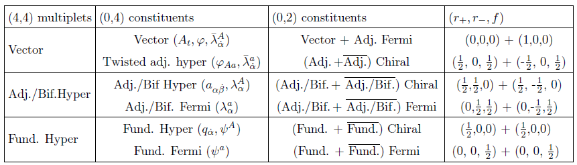
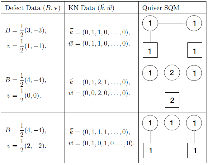
We revisit the localization computation of the expectation values of ’t Hooft operators in N = 2* SU(N) theory on R3 × S1. We show that the part of the answer arising from “monopole bubbling” on R3 can be understood as an equivariant integral over a Kronheimer-Nakajima moduli space of instantons on an orbifold of C2. It can also be described as a Witten index of a certain supersymmetric quiver quantum mechanics with N = (4, 4) supersymmetry. The map between the defect data and the quiver quantum mechanics is worked out for all values of N. For the SU(2) theory, we compute several examples of these line defect expectation values using the Witten index formula and confirm that the expressions agree with the formula derived by Okuda, Ito and Taki. In addition, we present a Type IIB construction — involving D1-D3-NS5-branes — for monopole bubbling in N = 2* SU(N) SYM and demonstrate how the quiver quantum mechanics arises in this brane picture.
- Research Organization:
- Rutgers Univ., Piscataway, NJ (United States)
- Sponsoring Organization:
- USDOE Office of Science (SC), High Energy Physics (HEP)
- Grant/Contract Number:
- SC0010008
- OSTI ID:
- 1502391
- Journal Information:
- Journal of High Energy Physics (Online), Vol. 2018, Issue 9; ISSN 1029-8479
- Publisher:
- Springer BerlinCopyright Statement
- Country of Publication:
- United States
- Language:
- English
Web of Science
Coulomb branch quantization and abelianized monopole bubbling
|
journal | October 2019 |
’t Hooft defects and wall crossing in SQM
|
journal | October 2019 |
| On Monopole Bubbling Contributions to 't Hooft Loops | text | January 2019 |
| 't Hooft Defects and Wall Crossing in SQM | text | January 2018 |
Quantum line defects and refined BPS spectra
|
journal | October 2019 |
Similar Records
’t Hooft defects and wall crossing in SQM
Monopole bubbling via string theory