Alfvén wave collisions, the fundamental building block of plasma turbulence. II. Numerical solution
Abstract
Here, this paper presents the numerical verification of an asymptotic analytical solution for the nonlinear interaction between counterpropagating Alfvén waves, the fundamental building block of astrophysical plasma turbulence. The analytical solution, derived in the weak turbulence limit using the equations of incompressible MHD, is compared to a nonlinear gyrokinetic simulation of an Alfvén wave collision. Finally, the agreement between these methods signifies that the incompressible solution satisfactorily describes the essential dynamics of the nonlinear energy transfer, even under the weakly collisional plasma conditions relevant to many astrophysical environments.
- Authors:
-
- Univ. of Iowa, Iowa City, IA (United States)
- Univ. of Maryland, College Park, MD (United States)
- Publication Date:
- Research Org.:
- Oak Ridge National Laboratory (ORNL), Oak Ridge, TN (United States). Oak Ridge Leadership Computing Facility (OLCF)
- Sponsoring Org.:
- USDOE Office of Science (SC)
- OSTI Identifier:
- 1565008
- Resource Type:
- Accepted Manuscript
- Journal Name:
- Physics of Plasmas
- Additional Journal Information:
- Journal Volume: 20; Journal Issue: 7; Journal ID: ISSN 1070-664X
- Publisher:
- American Institute of Physics (AIP)
- Country of Publication:
- United States
- Language:
- English
- Subject:
- 70 PLASMA PHYSICS AND FUSION TECHNOLOGY
Citation Formats
Nielson, K. D., Howes, G. G., and Dorland, W. Alfvén wave collisions, the fundamental building block of plasma turbulence. II. Numerical solution. United States: N. p., 2013.
Web. doi:10.1063/1.4812807.
Nielson, K. D., Howes, G. G., & Dorland, W. Alfvén wave collisions, the fundamental building block of plasma turbulence. II. Numerical solution. United States. https://doi.org/10.1063/1.4812807
Nielson, K. D., Howes, G. G., and Dorland, W. Mon .
"Alfvén wave collisions, the fundamental building block of plasma turbulence. II. Numerical solution". United States. https://doi.org/10.1063/1.4812807. https://www.osti.gov/servlets/purl/1565008.
@article{osti_1565008,
title = {Alfvén wave collisions, the fundamental building block of plasma turbulence. II. Numerical solution},
author = {Nielson, K. D. and Howes, G. G. and Dorland, W.},
abstractNote = {Here, this paper presents the numerical verification of an asymptotic analytical solution for the nonlinear interaction between counterpropagating Alfvén waves, the fundamental building block of astrophysical plasma turbulence. The analytical solution, derived in the weak turbulence limit using the equations of incompressible MHD, is compared to a nonlinear gyrokinetic simulation of an Alfvén wave collision. Finally, the agreement between these methods signifies that the incompressible solution satisfactorily describes the essential dynamics of the nonlinear energy transfer, even under the weakly collisional plasma conditions relevant to many astrophysical environments.},
doi = {10.1063/1.4812807},
journal = {Physics of Plasmas},
number = 7,
volume = 20,
place = {United States},
year = {Mon Jul 15 00:00:00 EDT 2013},
month = {Mon Jul 15 00:00:00 EDT 2013}
}
Web of Science
Figures / Tables:
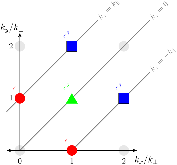 FIG. 1: Schematic diagram of the Fourier modes that play a role in the secular transfer of energy to small scales in an Alfvén wave collision. These key Fourier modes are the primary counterpropagating Alfvén waves (red circles), the secondary inherently nonlinear magnetic field fluctuation (green triangle), and the tertiarymore »
FIG. 1: Schematic diagram of the Fourier modes that play a role in the secular transfer of energy to small scales in an Alfvén wave collision. These key Fourier modes are the primary counterpropagating Alfvén waves (red circles), the secondary inherently nonlinear magnetic field fluctuation (green triangle), and the tertiarymore »
Works referenced in this record:
Alfvén wave collisions, the fundamental building block of plasma turbulence. I. Asymptotic solution
journal, July 2013
- Howes, G. G.; Nielson, K. D.
- Physics of Plasmas, Vol. 20, Issue 7
Nonlinear gyrokinetic equations for low-frequency electromagnetic waves in general plasma equilibria
journal, January 1982
- Frieman, E. A.
- Physics of Fluids, Vol. 25, Issue 3
Astrophysical Gyrokinetics: Basic Equations and Linear Theory
journal, November 2006
- Howes, Gregory G.; Cowley, Steven C.; Dorland, William
- The Astrophysical Journal, Vol. 651, Issue 1
Astrophysical Gyrokinetics: Kinetic and Fluid Turbulent Cascades in Magnetized Weakly Collisional Plasmas
journal, May 2009
- Schekochihin, A. A.; Cowley, S. C.; Dorland, W.
- The Astrophysical Journal Supplement Series, Vol. 182, Issue 1
A model of turbulence in magnetized plasmas: Implications for the dissipation range in the solar wind: DISSIPATION OF THE SOLAR WIND
journal, May 2008
- Howes, G. G.; Cowley, S. C.; Dorland, W.
- Journal of Geophysical Research: Space Physics, Vol. 113, Issue A5
Kinetic Simulations of Magnetized Turbulence in Astrophysical Plasmas
journal, February 2008
- Howes, G. G.; Dorland, W.; Cowley, S. C.
- Physical Review Letters, Vol. 100, Issue 6
Gyrokinetic Simulations of Solar Wind Turbulence from Ion to Electron Scales
journal, July 2011
- Howes, G. G.; TenBarge, J. M.; Dorland, W.
- Physical Review Letters, Vol. 107, Issue 3
A weakened cascade model for turbulence in astrophysical plasmas
journal, October 2011
- Howes, G. G.; TenBarge, J. M.; Dorland, W.
- Physics of Plasmas, Vol. 18, Issue 10
AstroGK: Astrophysical gyrokinetics code
journal, December 2010
- Numata, Ryusuke; Howes, Gregory G.; Tatsuno, Tomoya
- Journal of Computational Physics, Vol. 229, Issue 24
Linearized model Fokker–Planck collision operators for gyrokinetic simulations. I. Theory
journal, December 2008
- Abel, I. G.; Barnes, M.; Cowley, S. C.
- Physics of Plasmas, Vol. 15, Issue 12
Linearized model Fokker–Planck collision operators for gyrokinetic simulations. II. Numerical implementation and tests
journal, July 2009
- Barnes, M.; Abel, I. G.; Dorland, W.
- Physics of Plasmas, Vol. 16, Issue 7
The Hydromagnetic Equations
journal, July 1950
- Elsasser, Walter M.
- Physical Review, Vol. 79, Issue 1
Toward a theory of interstellar turbulence. 2: Strong alfvenic turbulence
journal, January 1995
- Goldreich, P.; Sridhar, S.
- The Astrophysical Journal, Vol. 438
Current Sheets and Collisionless Damping in Kinetic Plasma Turbulence
journal, June 2013
- TenBarge, J. M.; Howes, G. G.
- The Astrophysical Journal, Vol. 771, Issue 2
Nonlinear Phase Mixing and Phase-Space Cascade of Entropy in Gyrokinetic Plasma Turbulence
journal, June 2009
- Tatsuno, T.; Dorland, W.; Schekochihin, A. A.
- Physical Review Letters, Vol. 103, Issue 1
Toward Astrophysical Turbulence in the Laboratory
journal, December 2012
- Howes, G. G.; Drake, D. J.; Nielson, K. D.
- Physical Review Letters, Vol. 109, Issue 25
Using Synthetic Spacecraft data to Interpret Compressible Fluctuations in Solar wind Turbulence
journal, August 2012
- Klein, K. G.; Howes, G. G.; TenBarge, J. M.
- The Astrophysical Journal, Vol. 755, Issue 2
Resolving velocity space dynamics in continuum gyrokinetics
journal, March 2010
- Barnes, M.; Dorland, W.; Tatsuno, T.
- Physics of Plasmas, Vol. 17, Issue 3
Nonlinear phase mixing and phase-space cascade of entropy in gyrokinetic plasma turbulence
text, January 2008
- Tatsuno, T.; Dorland, W.; Schekochihin, A. A.
- arXiv
Gyrokinetic Simulations of Solar Wind Turbulence from Ion to Electron Scales
text, January 2011
- Howes, Gregory G.; TenBarge, Jason M.; Dorland, William
- arXiv
Works referencing / citing this record:
The Alfvénic nature of energy transfer mediation in localized, strongly nonlinear Alfvén wavepacket collisions
journal, January 2018
- Verniero, J. L.; Howes, G. G.
- Journal of Plasma Physics, Vol. 84, Issue 1
Laboratory space physics: Investigating the physics of space plasmas in the laboratory
journal, May 2018
- Howes, Gregory G.
- Physics of Plasmas, Vol. 25, Issue 5
On the ion-inertial-range density-power spectra in solar wind turbulence
journal, January 2019
- Treumann, Rudolf A.; Baumjohann, Wolfgang; Narita, Yasuhito
- Annales Geophysicae, Vol. 37, Issue 2
Nonlinear energy transfer and current sheet development in localized Alfven wavepacket collisions in the strong turbulence limit
text, January 2017
- Verniero, J. L.; Howes, G. G.; Klein, K. G.
- arXiv
Spatially Localized Particle Energization by Landau Damping in Current Sheets Produced by Strong Alfven Wave Collisions
text, January 2017
- Howes, Gregory G.; McCubbin, Andrew J.; Klein, Kristopher G.
- arXiv
The Alfvenic nature of energy transfer mediation in localized, strongly nonlinear Alfven wavepacket collisions
text, January 2017
- Verniero, J. L.; Howes, G. G.
- arXiv
Laboratory Space Physics: Investigating the Physics of Space Plasmas in the Laboratory
text, January 2018
- Howes, Gregory G.
- arXiv
Collisionless energy transfer in kinetic turbulence: field-particle correlations in Fourier space
text, January 2019
- Li, Tak Chu; Howes, Gregory G.; Klein, Kristopher G.
- arXiv
On the ion-inertial range density power spectra in solar wind turbulence
posted_content, December 2018
- Treumann, Rudolf A.; Baumjohann, Wolfgang; Narita, Yasuhito
- Annales Geophysicae
Figures / Tables found in this record:

 Search WorldCat to find libraries that may hold this journal
Search WorldCat to find libraries that may hold this journal