Application of Quantum Annealing to Nurse Scheduling Problem
Abstract
Quantum annealing is a promising heuristic method to solve combinatorial optimization problems, and efforts to quantify performance on real-world problems provide insights into how this approach may be best used in practice. We investigate the empirical performance of quantum annealing to solve the Nurse Scheduling Problem (NSP) with hard constraints using the D-Wave 2000Q quantum annealing device. NSP seeks the optimal assignment for a set of nurses to shifts under an accompanying set of constraints on schedule and personnel. After reducing NSP to a novel Ising-type Hamiltonian, we evaluate the solution quality obtained from the D-Wave 2000Q against the constraint requirements as well as the diversity of solutions. For the test problems explored here, our results indicate that quantum annealing recovers satisfying solutions for NSP and suggests the heuristic method is potentially achievable for practical use. Moreover, we observe that solution quality can be greatly improved through the use of reverse annealing, in which it is possible to refine returned results by using the annealing process a second time. We compare the performance of NSP using both forward and reverse annealing methods and describe how this approach might be used in practice.
- Authors:
-
[1];
[3]
- Osaka Univ. (Japan)
- Univ. of Tennessee, Knoxville, TN (United States)
- Oak Ridge National Lab. (ORNL), Oak Ridge, TN (United States)
- Publication Date:
- Research Org.:
- Oak Ridge National Lab. (ORNL), Oak Ridge, TN (United States)
- Sponsoring Org.:
- USDOE Office of Science (SC), Advanced Scientific Computing Research (ASCR)
- OSTI Identifier:
- 1560436
- Grant/Contract Number:
- AC05-00OR22725
- Resource Type:
- Accepted Manuscript
- Journal Name:
- Scientific Reports
- Additional Journal Information:
- Journal Volume: 9; Journal Issue: 1; Journal ID: ISSN 2045-2322
- Publisher:
- Nature Publishing Group
- Country of Publication:
- United States
- Language:
- English
- Subject:
- 97 MATHEMATICS AND COMPUTING
Citation Formats
Ikeda, Kazuki, Nakamura, Yuma, and Humble, Travis S. Application of Quantum Annealing to Nurse Scheduling Problem. United States: N. p., 2019.
Web. doi:10.1038/s41598-019-49172-3.
Ikeda, Kazuki, Nakamura, Yuma, & Humble, Travis S. Application of Quantum Annealing to Nurse Scheduling Problem. United States. https://doi.org/10.1038/s41598-019-49172-3
Ikeda, Kazuki, Nakamura, Yuma, and Humble, Travis S. Fri .
"Application of Quantum Annealing to Nurse Scheduling Problem". United States. https://doi.org/10.1038/s41598-019-49172-3. https://www.osti.gov/servlets/purl/1560436.
@article{osti_1560436,
title = {Application of Quantum Annealing to Nurse Scheduling Problem},
author = {Ikeda, Kazuki and Nakamura, Yuma and Humble, Travis S.},
abstractNote = {Quantum annealing is a promising heuristic method to solve combinatorial optimization problems, and efforts to quantify performance on real-world problems provide insights into how this approach may be best used in practice. We investigate the empirical performance of quantum annealing to solve the Nurse Scheduling Problem (NSP) with hard constraints using the D-Wave 2000Q quantum annealing device. NSP seeks the optimal assignment for a set of nurses to shifts under an accompanying set of constraints on schedule and personnel. After reducing NSP to a novel Ising-type Hamiltonian, we evaluate the solution quality obtained from the D-Wave 2000Q against the constraint requirements as well as the diversity of solutions. For the test problems explored here, our results indicate that quantum annealing recovers satisfying solutions for NSP and suggests the heuristic method is potentially achievable for practical use. Moreover, we observe that solution quality can be greatly improved through the use of reverse annealing, in which it is possible to refine returned results by using the annealing process a second time. We compare the performance of NSP using both forward and reverse annealing methods and describe how this approach might be used in practice.},
doi = {10.1038/s41598-019-49172-3},
journal = {Scientific Reports},
number = 1,
volume = 9,
place = {United States},
year = {Fri Sep 06 00:00:00 EDT 2019},
month = {Fri Sep 06 00:00:00 EDT 2019}
}
Free Publicly Available Full Text
Publisher's Version of Record
Other availability
Search WorldCat to find libraries that may hold this journal
Cited by: 36 works
Citation information provided by
Web of Science
Web of Science
Figures / Tables:
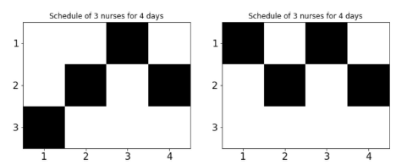Figure 1: Graphical examples of the computed shift schedules for the case of $N$ = 3 nurses for $D$ = 4 days. A black square indicates that a nurse is scheduled to work. The horizontal axes labels the days and the vertical axes labels the nurses. Te left figure representsmore »
All figures and tables
(10 total)
Save to My Library
You must Sign In or Create an Account in order to save documents to your library.
Works referenced in this record:
Traffic Flow Optimization Using a Quantum Annealer
journal, December 2017
- Neukart, Florian; Compostella, Gabriele; Seidel, Christian
- Frontiers in ICT, Vol. 4
An integrated programming and development environment for adiabatic quantum optimization
journal, January 2014
- S. Humble, T.; J. McCaskey, A.; S. Bennink, R.
- Computational Science & Discovery, Vol. 7, Issue 1
A Quantum Adiabatic Evolution Algorithm Applied to Random Instances of an NP-Complete Problem
journal, April 2001
- Farhi, E.; Goldstone, J.; Gutmann, S.
- Science, Vol. 292, Issue 5516
An approach to quantum-computational hydrologic inverse analysis
journal, May 2018
- O’Malley, Daniel
- Scientific Reports, Vol. 8, Issue 1
Improving solutions by embedding larger subproblems in a D-Wave quantum annealer
journal, February 2019
- Okada, Shuntaro; Ohzeki, Masayuki; Terabe, Masayoshi
- Scientific Reports, Vol. 9, Issue 1
Sherrington-Kirkpatrick model in a transverse field: Absence of replica symmetry breaking due to quantum fluctuations
journal, June 1989
- Ray, P.; Chakrabarti, B. K.; Chakrabarti, Arunava
- Physical Review B, Vol. 39, Issue 16
Quantum annealing in the transverse Ising model
journal, November 1998
- Kadowaki, Tadashi; Nishimori, Hidetoshi
- Physical Review E, Vol. 58, Issue 5
Adiabatic Quantum Computation Is Equivalent to Standard Quantum Computation
journal, January 2008
- Aharonov, Dorit; van Dam, Wim; Kempe, Julia
- SIAM Review, Vol. 50, Issue 4
Quantum Optimization of Fully Connected Spin Glasses
journal, September 2015
- Venturelli, Davide; Mandrà, Salvatore; Knysh, Sergey
- Physical Review X, Vol. 5, Issue 3
Benchmarking treewidth as a practical component of tensor network simulations
journal, December 2018
- Dumitrescu, Eugene F.; Fisher, Allison L.; Goodrich, Timothy D.
- PLOS ONE, Vol. 13, Issue 12
Quantum annealing with manufactured spins
journal, May 2011
- Johnson, M. W.; Amin, M. H. S.; Gildert, S.
- Nature, Vol. 473, Issue 7346
Ising formulations of many NP problems
journal, January 2014
- Lucas, Andrew
- Frontiers in Physics, Vol. 2
Solving the Optimal Trading Trajectory Problem Using a Quantum Annealer
journal, September 2016
- Rosenberg, Gili; Haghnegahdar, Poya; Goddard, Phil
- IEEE Journal of Selected Topics in Signal Processing, Vol. 10, Issue 6
Identifying the minor set cover of dense connected bipartite graphs via random matching edge sets
journal, February 2017
- Hamilton, Kathleen E.; Humble, Travis S.
- Quantum Information Processing, Vol. 16, Issue 4
Works referencing / citing this record:
Foundation of quantum optimal transport and applications
journal, November 2019
- Ikeda, Kazuki
- Quantum Information Processing, Vol. 19, Issue 1
Figures/Tables have been extracted from DOE-funded journal article accepted manuscripts.