Measuring the Error in Approximating the Sub-Level Set Topology of Sampled Scalar Data
Abstract
This paper studies here the influence of the definition of neighborhoods and methods used for creating point connectivity on topological analysis of scalar functions. It is assumed that a scalar function is known only at a finite set of points with associated function values. In order to utilize topological approaches to analyze the scalar-valued point set, it is necessary to choose point neighborhoods and, usually, point connectivity to meaningfully determine critical-point behavior for the point set. Two distances are used to measure the difference in topology when different point neighborhoods and means to define connectivity are used: (i) the bottleneck distance for persistence diagrams and (ii) the distance between merge trees. Usually, these distances define how different scalar functions are with respect to their topology. These measures, when properly adapted to point sets coupled with a definition of neighborhood and connectivity, make it possible to understand how topological characteristics depend on connectivity. Noise is another aspect considered. Five types of neighborhoods and connectivity are discussed: (i) the Delaunay triangulation; (ii) the relative neighborhood graph; (iii) the Gabriel graph; (iv) the k-nearest-neighbor (KNN) neighborhood; and (v) the Vietoris–Rips complex. It is discussed in detail how topological characterizations depend on the chosenmore »
- Authors:
-
- Lawrence Berkeley National Lab. (LBNL), Berkeley, CA (United States); National Lab. Astana (Kazakhstan)
- Univ. of California, Los Angeles, CA (United States). Dept. of Mathematics; Kazakh-British Technical Univ., Almaty (Kazakhstan)
- Lawrence Berkeley National Lab. (LBNL), Berkeley, CA (United States)
- Univ. of California, Davis, CA (United States). Dept. of Computer Science
- Publication Date:
- Research Org.:
- Lawrence Berkeley National Lab. (LBNL), Berkeley, CA (United States)
- Sponsoring Org.:
- USDOE Office of Science (SC), Advanced Scientific Computing Research (ASCR); Ministry of Education and Science of the Republic of Kazakhstan
- OSTI Identifier:
- 1505518
- Grant/Contract Number:
- AC02-05CH11231; 0115PK03029
- Resource Type:
- Accepted Manuscript
- Journal Name:
- International Journal of Computational Geometry & Applications
- Additional Journal Information:
- Journal Volume: 28; Journal Issue: 01; Journal ID: ISSN 0218-1959
- Publisher:
- World Scientific
- Country of Publication:
- United States
- Language:
- English
- Subject:
- 97 MATHEMATICS AND COMPUTING; sub-level set topology; error quantification; topological structures
Citation Formats
Beketayev, Kenes, Yeliussizov, Damir, Morozov, Dmitriy, Weber, Gunther H., and Hamann, Bernd. Measuring the Error in Approximating the Sub-Level Set Topology of Sampled Scalar Data. United States: N. p., 2018.
Web. doi:10.1142/S0218195918500036.
Beketayev, Kenes, Yeliussizov, Damir, Morozov, Dmitriy, Weber, Gunther H., & Hamann, Bernd. Measuring the Error in Approximating the Sub-Level Set Topology of Sampled Scalar Data. United States. https://doi.org/10.1142/S0218195918500036
Beketayev, Kenes, Yeliussizov, Damir, Morozov, Dmitriy, Weber, Gunther H., and Hamann, Bernd. Thu .
"Measuring the Error in Approximating the Sub-Level Set Topology of Sampled Scalar Data". United States. https://doi.org/10.1142/S0218195918500036. https://www.osti.gov/servlets/purl/1505518.
@article{osti_1505518,
title = {Measuring the Error in Approximating the Sub-Level Set Topology of Sampled Scalar Data},
author = {Beketayev, Kenes and Yeliussizov, Damir and Morozov, Dmitriy and Weber, Gunther H. and Hamann, Bernd},
abstractNote = {This paper studies here the influence of the definition of neighborhoods and methods used for creating point connectivity on topological analysis of scalar functions. It is assumed that a scalar function is known only at a finite set of points with associated function values. In order to utilize topological approaches to analyze the scalar-valued point set, it is necessary to choose point neighborhoods and, usually, point connectivity to meaningfully determine critical-point behavior for the point set. Two distances are used to measure the difference in topology when different point neighborhoods and means to define connectivity are used: (i) the bottleneck distance for persistence diagrams and (ii) the distance between merge trees. Usually, these distances define how different scalar functions are with respect to their topology. These measures, when properly adapted to point sets coupled with a definition of neighborhood and connectivity, make it possible to understand how topological characteristics depend on connectivity. Noise is another aspect considered. Five types of neighborhoods and connectivity are discussed: (i) the Delaunay triangulation; (ii) the relative neighborhood graph; (iii) the Gabriel graph; (iv) the k-nearest-neighbor (KNN) neighborhood; and (v) the Vietoris–Rips complex. It is discussed in detail how topological characterizations depend on the chosen connectivity.},
doi = {10.1142/S0218195918500036},
journal = {International Journal of Computational Geometry & Applications},
number = 01,
volume = 28,
place = {United States},
year = {Thu Mar 29 00:00:00 EDT 2018},
month = {Thu Mar 29 00:00:00 EDT 2018}
}
Figures / Tables:
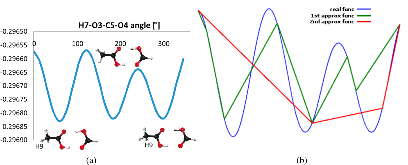 Fig. 1: (a) Rotation of the methyl group of the molecule of dimer of formic and acetic acid produces the potential energy function, i.e., the real function. (b) Although the first approximated function deviates from the real function, it still preserves the correct number of minima — three — thusmore »
Fig. 1: (a) Rotation of the methyl group of the molecule of dimer of formic and acetic acid produces the potential energy function, i.e., the real function. (b) Although the first approximated function deviates from the real function, it still preserves the correct number of minima — three — thusmore »
Works referenced in this record:
Empty region graphs
journal, April 2009
- Cardinal, Jean; Collette, Sébastien; Langerman, Stefan
- Computational Geometry, Vol. 42, Issue 3
Visualization of High-Dimensional Point Clouds Using Their Density Distribution's Topology
journal, November 2011
- Oesterling, P.; Heine, C.; Janicke, H.
- IEEE Transactions on Visualization and Computer Graphics, Vol. 17, Issue 11
Hierarchical Morse--Smale Complexes for Piecewise Linear 2-Manifolds
journal, May 2003
- Edelsbrunner, Herbert; Harer, John; Zomorodian, Afra
- Discrete and Computational Geometry, Vol. 30, Issue 1
Visualization of Barrier Tree Sequences
journal, September 2006
- Heine, Christian; Scheuermann, Gerik; Flamm, Christoph
- IEEE Transactions on Visualization and Computer Graphics, Vol. 12, Issue 5
Computing contour trees in all dimensions
journal, February 2003
- Carr, Hamish; Snoeyink, Jack; Axen, Ulrike
- Computational Geometry, Vol. 24, Issue 2
Topological Landscapes: A Terrain Metaphor for Scientific Data
journal, November 2007
- Weber, Gunther; Bremer, Peer-Timo; Pascucci, Valerio
- IEEE Transactions on Visualization and Computer Graphics, Vol. 13, Issue 6
Extraction of Dominant Extremal Structures in Volumetric Data Using Separatrix Persistence
journal, October 2012
- Günther, D.; Seidel, H. -P.; Weinkauf, T.
- Computer Graphics Forum, Vol. 31, Issue 8
Describing shapes by geometrical-topological properties of real functions
journal, October 2008
- Biasotti, S.; De Floriani, L.; Falcidieno, B.
- ACM Computing Surveys, Vol. 40, Issue 4
Topological saliency
journal, November 2013
- Doraiswamy, Harish; Shivashankar, Nithin; Natarajan, Vijay
- Computers & Graphics, Vol. 37, Issue 7
Applying Manifold Learning to Plotting Approximate Contour Trees
journal, November 2009
- Takahashi, S.; Fujishiro, I.; Okada, M.
- IEEE Transactions on Visualization and Computer Graphics, Vol. 15, Issue 6
�ber den h�heren Zusammenhang kompakter R�ume und eine Klasse von zusammenhangstreuen Abbildungen
journal, December 1927
- Vietoris, L.
- Mathematische Annalen, Vol. 97, Issue 1
A Scale Space Based Persistence Measure for Critical Points in 2D Scalar Fields
journal, December 2011
- Reininghaus, J.; Kotava, N.; Gunther, D.
- IEEE Transactions on Visualization and Computer Graphics, Vol. 17, Issue 12
A compendium of potential energy maps of zeolites and molecular sieves
journal, April 1996
- Keffer, D.; Gupta, Vishwas; Kim, David
- Journal of Molecular Graphics, Vol. 14, Issue 2
Topological Landscape Ensembles for Visualization of Scalar-Valued Functions
journal, June 2010
- Harvey, William; Wang, Yusu
- Computer Graphics Forum, Vol. 29, Issue 3
Comparison of designs for computer experiments
journal, March 2006
- Bursztyn, Dizza; Steinberg, David M.
- Journal of Statistical Planning and Inference, Vol. 136, Issue 3
Computing contour trees in all dimensions
text, January 2003
- Ulrike, Axen,; Jack, Snoeyink,; Hamish, Carr,
- The University of North Carolina at Chapel Hill University Libraries
Figures / Tables found in this record:

 Search WorldCat to find libraries that may hold this journal
Search WorldCat to find libraries that may hold this journal