Wave kinetics of drift-wave turbulence and zonal flows beyond the ray approximation
Abstract
Inhomogeneous drift-wave turbulence can be modeled as an effective plasma where drift waves act as quantumlike particles and the zonal-flow velocity serves as a collective field through which they interact. This effective plasma can be described by a Wigner-Moyal equation (WME), which generalizes the quasilinear wave-kinetic equation (WKE) to the full-wave regime, i.e., resolves the wavelength scale. Unlike waves governed by manifestly quantumlike equations, whose WMEs can be borrowed from quantum mechanics and are commonly known, drift waves have Hamiltonians very different from those of conventional quantum particles. This causes unusual phase-space dynamics that is typically not captured by the WKE. We demonstrate how to correctly model this dynamics with the WME instead. Specifically, we report full-wave phase-space simulations of the zonal-flow formation (zonostrophic instability), deterioration (tertiary instability), and the so-called predator-prey oscillations. We also show how the WME facilitates analysis of these phenomena, namely, (i) we show that full-wave effects critically affect the zonostrophic instability, particularly its nonlinear stage and saturation; (ii) we derive the tertiary-instability growth rate; and (iii) we demonstrate that, with full-wave effects retained, the predator-prey oscillations do not require zonal-flow collisional damping, contrary to previous studies. In conclusion, we also show how the famous Rayleigh-Kuomore »
- Authors:
-
- Princeton Univ., Princeton, NJ (United States); Princeton Plasma Physics Lab. (PPPL), Princeton, NJ (United States)
- Princeton Plasma Physics Lab. (PPPL), Princeton, NJ (United States)
- Sandia National Lab. (SNL-NM), Albuquerque, NM (United States)
- Publication Date:
- Research Org.:
- Princeton Plasma Physics Laboratory (PPPL), Princeton, NJ (United States)
- Sponsoring Org.:
- USDOE
- OSTI Identifier:
- 1440782
- Alternate Identifier(s):
- OSTI ID: 1439383
- Grant/Contract Number:
- AC02-09CH11466; NA0003525
- Resource Type:
- Accepted Manuscript
- Journal Name:
- Physical Review E
- Additional Journal Information:
- Journal Volume: 97; Journal Issue: 5; Journal ID: ISSN 2470-0045
- Publisher:
- American Physical Society (APS)
- Country of Publication:
- United States
- Language:
- English
- Subject:
- 70 PLASMA PHYSICS AND FUSION TECHNOLOGY
Citation Formats
Zhu, Hongxuan, Zhou, Yao, Ruiz, D. E., and Dodin, I. Y. Wave kinetics of drift-wave turbulence and zonal flows beyond the ray approximation. United States: N. p., 2018.
Web. doi:10.1103/PhysRevE.97.053210.
Zhu, Hongxuan, Zhou, Yao, Ruiz, D. E., & Dodin, I. Y. Wave kinetics of drift-wave turbulence and zonal flows beyond the ray approximation. United States. https://doi.org/10.1103/PhysRevE.97.053210
Zhu, Hongxuan, Zhou, Yao, Ruiz, D. E., and Dodin, I. Y. Tue .
"Wave kinetics of drift-wave turbulence and zonal flows beyond the ray approximation". United States. https://doi.org/10.1103/PhysRevE.97.053210. https://www.osti.gov/servlets/purl/1440782.
@article{osti_1440782,
title = {Wave kinetics of drift-wave turbulence and zonal flows beyond the ray approximation},
author = {Zhu, Hongxuan and Zhou, Yao and Ruiz, D. E. and Dodin, I. Y.},
abstractNote = {Inhomogeneous drift-wave turbulence can be modeled as an effective plasma where drift waves act as quantumlike particles and the zonal-flow velocity serves as a collective field through which they interact. This effective plasma can be described by a Wigner-Moyal equation (WME), which generalizes the quasilinear wave-kinetic equation (WKE) to the full-wave regime, i.e., resolves the wavelength scale. Unlike waves governed by manifestly quantumlike equations, whose WMEs can be borrowed from quantum mechanics and are commonly known, drift waves have Hamiltonians very different from those of conventional quantum particles. This causes unusual phase-space dynamics that is typically not captured by the WKE. We demonstrate how to correctly model this dynamics with the WME instead. Specifically, we report full-wave phase-space simulations of the zonal-flow formation (zonostrophic instability), deterioration (tertiary instability), and the so-called predator-prey oscillations. We also show how the WME facilitates analysis of these phenomena, namely, (i) we show that full-wave effects critically affect the zonostrophic instability, particularly its nonlinear stage and saturation; (ii) we derive the tertiary-instability growth rate; and (iii) we demonstrate that, with full-wave effects retained, the predator-prey oscillations do not require zonal-flow collisional damping, contrary to previous studies. In conclusion, we also show how the famous Rayleigh-Kuo criterion, which has been missing in wave-kinetic theories of drift-wave turbulence, emerges from the WME.},
doi = {10.1103/PhysRevE.97.053210},
journal = {Physical Review E},
number = 5,
volume = 97,
place = {United States},
year = {Tue May 29 00:00:00 EDT 2018},
month = {Tue May 29 00:00:00 EDT 2018}
}
Free Publicly Available Full Text
Publisher's Version of Record
Other availability
Search WorldCat to find libraries that may hold this journal
Cited by: 18 works
Citation information provided by
Web of Science
Web of Science
Figures / Tables:
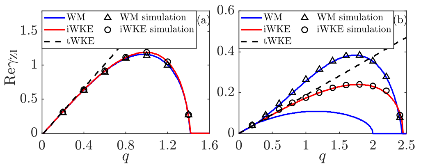FIG. 1: $γ$ZI($q$) at $β$ = 1 for two equilibria: (a) $\mathcal{W}$1 with $\mathcal{N}$ = 50 and $p$$f$ = 1; (b) $\mathcal{W}$2 with $k$$x$ = 2, $k$$y$ = 1, and $\mathcal{N}$ = 100/(2$π$)2. Shown are the analytical results obtained from the WM (blue), iWKE (red), and tWKE (dashed) models, andmore »
All figures and tables
(5 total)
Save to My Library
You must Sign In or Create an Account in order to save documents to your library.
Works referenced in this record:
Noncurvature-driven modes in a transport barrier
journal, June 2005
- Rogers, B. N.; Dorland, W.
- Physics of Plasmas, Vol. 12, Issue 6
Numerical Investigation of the Instability and Nonlinear Evolution of Narrow-Band Directional Ocean Waves
journal, June 2010
- Eliasson, Bengt; Shukla, P. K.
- Physical Review Letters, Vol. 105, Issue 1
Spatio-temporal evolution of the L → I → H transition
journal, September 2012
- Miki, K.; Diamond, P. H.; Gürcan, Ö. D.
- Physics of Plasmas, Vol. 19, Issue 9
Zonal-flow dynamics from a phase-space perspective
journal, December 2016
- Ruiz, D. E.; Parker, J. B.; Shi, E. L.
- Physics of Plasmas, Vol. 23, Issue 12
Zonal flow as pattern formation
journal, October 2013
- Parker, Jeffrey B.; Krommes, John A.
- Physics of Plasmas, Vol. 20, Issue 10
Interactions of disparate scales in drift-wave turbulence
journal, December 2000
- Krommes, John A.; Kim, Chang-Bae
- Physical Review E, Vol. 62, Issue 6
Dynamics of zonal flows: failure of wave-kinetic theory, and new geometrical optics approximations
journal, November 2016
- Parker, Jeffrey B.
- Journal of Plasma Physics, Vol. 82, Issue 6
Gyrokinetic continuum simulation of turbulence in a straight open-field-line plasma
journal, May 2017
- Shi, E. L.; Hammett, G. W.; Stoltzfus-Dueck, T.
- Journal of Plasma Physics, Vol. 83, Issue 3
Dynamics of zonal flow saturation in strong collisionless drift wave turbulence
journal, November 2002
- Kim, Eun-jin; Diamond, P. H.
- Physics of Plasmas, Vol. 9, Issue 11
Quasiparticle Approach to the Modulational Instability of Drift Waves Coupling to Zonal Flows
journal, April 2005
- Trines, R.; Bingham, R.; Silva, L. O.
- Physical Review Letters, Vol. 94, Issue 16
Mathematical basis for analysis of partially coherent wave propagation in nonlinear, non-instantaneous, Kerr media
journal, July 2008
- Semenov, V.; Lisak, M.; Anderson, D.
- Journal of Physics A: Mathematical and Theoretical, Vol. 41, Issue 33
Scalar Wigner theory for polarized light in nonlinear Kerr media
journal, January 2013
- Hansson, Tobias; Wallin, Erik; Brodin, Gert
- Journal of the Optical Society of America B, Vol. 30, Issue 6
Coherent Structure Phenomena in Drift Wave–Zonal Flow Turbulence
journal, January 2000
- Smolyakov, A. I.; Diamond, P. H.; Malkov, M.
- Physical Review Letters, Vol. 84, Issue 3
Optical wave turbulence: Towards a unified nonequilibrium thermodynamic formulation of statistical nonlinear optics
journal, September 2014
- Picozzi, A.; Garnier, J.; Hansson, T.
- Physics Reports, Vol. 542, Issue 1
On the stability of drift wave spectra with respect to zonal flow excitation
journal, May 2001
- Malkov, M. A.; Diamond, P. H.; Smolyakov, A.
- Physics of Plasmas, Vol. 8, Issue 5
Coherent structures in ion temperature gradient turbulence-zonal flow
journal, October 2014
- Singh, Rameswar; Singh, R.; Kaw, P.
- Physics of Plasmas, Vol. 21, Issue 10
Generalized action invariants for drift waves-zonal flow systems
journal, December 1999
- Smolyakov, A. I.; Diamond, P. H.
- Physics of Plasmas, Vol. 6, Issue 12
Generation of zonal flows through symmetry breaking of statistical homogeneity
journal, March 2014
- Parker, Jeffrey B.; Krommes, John A.
- New Journal of Physics, Vol. 16, Issue 3
Quantum mechanics as a statistical theory
journal, January 1949
- Moyal, J. E.
- Mathematical Proceedings of the Cambridge Philosophical Society, Vol. 45, Issue 1
Identification of Zonal Flows in a Toroidal Plasma
journal, October 2004
- Fujisawa, A.; Itoh, K.; Iguchi, H.
- Physical Review Letters, Vol. 93, Issue 16
Landau damping and coherent structures in narrow-banded deep water gravity waves
journal, April 2003
- Onorato, Miguel; Osborne, Alfred; Fedele, Renato
- Physical Review E, Vol. 67, Issue 4
Detection of Zero-Mean-Frequency Zonal Flows in the Core of a High-Temperature Tokamak Plasma
journal, September 2006
- Gupta, D. K.; Fonck, R. J.; McKee, G. R.
- Physical Review Letters, Vol. 97, Issue 12
A review of zonal flow experiments
journal, December 2008
- Fujisawa, Akihide
- Nuclear Fusion, Vol. 49, Issue 1
On the Quantum Correction For Thermodynamic Equilibrium
journal, June 1932
- Wigner, E.
- Physical Review, Vol. 40, Issue 5
Integrability and Conservation Laws for the Nonlinear Evolution Equations of Partially Coherent Waves in Noninstantaneous Kerr Media
journal, February 2012
- Hansson, T.; Lisak, M.; Anderson, D.
- Physical Review Letters, Vol. 108, Issue 6
Generation and Stability of Zonal Flows in Ion-Temperature-Gradient Mode Turbulence
journal, December 2000
- Rogers, B. N.; Dorland, W.; Kotschenreuther, M.
- Physical Review Letters, Vol. 85, Issue 25
Bifurcation in electrostatic resistive drift wave turbulence
journal, October 2007
- Numata, Ryusuke; Ball, Rowena; Dewar, Robert L.
- Physics of Plasmas, Vol. 14, Issue 10
Coherent nonlinear structures of drift wave turbulence modulated by zonal flows
journal, December 2001
- Kaw, Predhiman; Singh, Raghvendra; Diamond, P. H.
- Plasma Physics and Controlled Fusion, Vol. 44, Issue 1
On non-local energy transfer via zonal flow in the Dimits shift
journal, October 2017
- St-Onge, Denis A.
- Journal of Plasma Physics, Vol. 83, Issue 5
Statistical theory for incoherent light propagation in nonlinear media
journal, February 2002
- Hall, B.; Lisak, M.; Anderson, D.
- Physical Review E, Vol. 65, Issue 3
An analytic model for limiting high density LH transition by the onset of the tertiary instability
journal, July 2016
- Singh, Raghvendra; Jhang, Hogun; Kaang, Helen H.
- Physics of Plasmas, Vol. 23, Issue 7
Zonal flows in plasma—a review
journal, April 2005
- Diamond, P. H.; Itoh, S-I; Itoh, K.
- Plasma Physics and Controlled Fusion, Vol. 47, Issue 5
Zonal flow generation by parametric instability in magnetized plasmas and geostrophic fluids
journal, May 2000
- Smolyakov, A. I.; Diamond, P. H.; Shevchenko, V. I.
- Physics of Plasmas, Vol. 7, Issue 5
Wigner-Moyal description of free variable mass Klein-Gordon fields
journal, October 2005
- Santos, J. P.; Silva, L. O.
- Journal of Mathematical Physics, Vol. 46, Issue 10
Zonostrophic Instability
journal, May 2012
- Srinivasan, Kaushik; Young, W. R.
- Journal of the Atmospheric Sciences, Vol. 69, Issue 5
Stationary Zonal Flows during the Formation of the Edge Transport Barrier in the JET Tokamak
journal, February 2016
- Hillesheim, J. C.; Delabie, E.; Meyer, H.
- Physical Review Letters, Vol. 116, Issue 6
Developments in the gyrofluid approach to Tokamak turbulence simulations
journal, August 1993
- Hammett, G. W.; Beer, M. A.; Dorland, W.
- Plasma Physics and Controlled Fusion, Vol. 35, Issue 8
Rossby and drift wave turbulence and zonal flows: The Charney–Hasegawa–Mima model and its extensions
journal, December 2015
- Connaughton, Colm; Nazarenko, Sergey; Quinn, Brenda
- Physics Reports, Vol. 604
Self-Regulating Shear Flow Turbulence: A Paradigm for the L to H Transition
journal, April 1994
- Diamond, P. H.; Liang, Y. -M.; Carreras, B. A.
- Physical Review Letters, Vol. 72, Issue 16
Zonal Flows and Transient Dynamics of the Transition
journal, May 2003
- Kim, Eun-jin; Diamond, P. H.
- Physical Review Letters, Vol. 90, Issue 18
White-Light Parametric Instabilities in Plasmas
journal, June 2007
- Santos, J. E.; Silva, L. O.; Bingham, R.
- Physical Review Letters, Vol. 98, Issue 23
Statistical State Dynamics of Jet–Wave Coexistence in Barotropic Beta-Plane Turbulence
journal, May 2016
- Constantinou, Navid C.; Farrell, Brian F.; Ioannou, Petros J.
- Journal of the Atmospheric Sciences, Vol. 73, Issue 5
White-light parametric instabilities in plasmas
text, January 2007
- Santos, J. E.; Silva, L. O.; Bingham, R.
- arXiv
Bifurcation in electrostatic resistive drift wave turbulence
text, January 2007
- Numata, Ryusuke; Ball, Rowena; Dewar, Robert L.
- arXiv
A Scalar Wigner Theory for Polarized Light in Nonlinear Kerr Media
text, January 2012
- Hansson, T.; Wallin, E.; Brodin, G.
- arXiv
Rossby and Drift Wave Turbulence and Zonal Flows: the Charney-Hasegawa-Mima model and its extensions
text, January 2014
- Connaughton, Colm; Nazarenko, Sergey; Quinn, Brenda
- arXiv
Statistical state dynamics of jet/wave coexistence in barotropic beta-plane turbulence
text, January 2015
- Constantinou, Navid C.; Farrell, Brian F.; Ioannou, Petros J.
- arXiv
Dynamics of Zonal Flows: Failure of Wave-Kinetic Theory, and New Geometrical Optics Approximations
text, January 2016
- Parker, Jeffrey B.
- arXiv
Gyrokinetic continuum simulation of turbulence in a straight open-field-line plasma
text, January 2017
- Shi, E. L.; Hammett, G. W.; Stoltzfus-Dueck, T.
- arXiv
On Nonlocal Energy Transfer via Zonal Flow in the Dimits Shift
text, January 2017
- St-Onge, Denis A.
- arXiv
Generalized Action Invariants for Drift Waves-Zonal Flow Systems
text, January 1999
- Smolyakov, A. I.; Diamond, P. H.
- arXiv
Works referencing / citing this record:
On the Rayleigh–Kuo criterion for the tertiary instability of zonal flows
journal, August 2018
- Zhu, Hongxuan; Zhou, Yao; Dodin, I. Y.
- Physics of Plasmas, Vol. 25, Issue 8
On the structure of the drifton phase space and its relation to the Rayleigh–Kuo criterion of the zonal-flow stability
journal, July 2018
- Zhu, Hongxuan; Zhou, Yao; Dodin, I. Y.
- Physics of Plasmas, Vol. 25, Issue 7
Formation of solitary zonal structures via the modulational instability of drift waves
journal, May 2019
- Zhou, Yao; Zhu, Hongxuan; Dodin, I. Y.
- Plasma Physics and Controlled Fusion, Vol. 61, Issue 7
Nonlinear saturation and oscillations of collisionless zonal flows
text, January 2019
- Zhu, Hongxuan; Zhou, Yao; Dodin, I. Y.
- Zenodo
Nonlinear saturation and oscillations of collisionless zonal flows
journal, June 2019
- Zhu, Hongxuan; Zhou, Yao; Dodin, I. Y.
- New Journal of Physics, Vol. 21, Issue 6
Nonlinear saturation and oscillations of collisionless zonal flows
text, January 2019
- Zhu, Hongxuan; Zhou, Yao; Dodin, I. Y.
- Zenodo
On the Rayleigh--Kuo criterion for the tertiary instability of zonal flows
text, January 2018
- Zhu, Hongxuan; Zhou, Yao; Dodin, I. Y.
- arXiv
Figures / Tables found in this record:
Figures/Tables have been extracted from DOE-funded journal article accepted manuscripts.