Induced Eddy Currents in Simple Conductive Geometries: Mathematical Formalism Describes the Excitation of Electrical Eddy Currents in a Time-Varying Magnetic Field
Abstract
In this paper, a complete mathematical formalism is introduced to describe the excitation of electrical eddy currents due to a time-varying magnetic field. The process works by applying a quasistatic approximation to Ampere's law and then segregating the magnetic field into impressed and induced terms. The result is a nonhomogeneous vector Helmholtz equation that can be analytically solved for many practical geometries. Four demonstration cases are then solved under a constant excitation field over all space—an infinite slab in one dimension, a longitudinal cylinder in two dimensions, a transverse cylinder in two dimensions, and a sphere in three dimensions. Numerical simulations are also performed in parallel with analytic computations, all of which verify the accuracy of the derived expressions.
- Authors:
-
- Univ. of Utah, Salt Lake City, UT (United States). Metallurgical Engineering
- Publication Date:
- Research Org.:
- Univ. of Utah, Salt Lake City, UT (United States)
- Sponsoring Org.:
- USDOE Advanced Research Projects Agency - Energy (ARPA-E)
- OSTI Identifier:
- 1433514
- Grant/Contract Number:
- AR0000411
- Resource Type:
- Accepted Manuscript
- Journal Name:
- IEEE Antennas and Propagation Magazine
- Additional Journal Information:
- Journal Volume: 60; Journal Issue: 1; Journal ID: ISSN 1045-9243
- Publisher:
- IEEE
- Country of Publication:
- United States
- Language:
- English
- Subject:
- 32 ENERGY CONSERVATION, CONSUMPTION, AND UTILIZATION; 36 MATERIALS SCIENCE; 72 PHYSICS OF ELEMENTARY PARTICLES AND FIELDS; eddy currents; quasistatics; current density
Citation Formats
Nagel, James R. Induced Eddy Currents in Simple Conductive Geometries: Mathematical Formalism Describes the Excitation of Electrical Eddy Currents in a Time-Varying Magnetic Field. United States: N. p., 2017.
Web. doi:10.1109/MAP.2017.2774206.
Nagel, James R. Induced Eddy Currents in Simple Conductive Geometries: Mathematical Formalism Describes the Excitation of Electrical Eddy Currents in a Time-Varying Magnetic Field. United States. https://doi.org/10.1109/MAP.2017.2774206
Nagel, James R. Fri .
"Induced Eddy Currents in Simple Conductive Geometries: Mathematical Formalism Describes the Excitation of Electrical Eddy Currents in a Time-Varying Magnetic Field". United States. https://doi.org/10.1109/MAP.2017.2774206. https://www.osti.gov/servlets/purl/1433514.
@article{osti_1433514,
title = {Induced Eddy Currents in Simple Conductive Geometries: Mathematical Formalism Describes the Excitation of Electrical Eddy Currents in a Time-Varying Magnetic Field},
author = {Nagel, James R.},
abstractNote = {In this paper, a complete mathematical formalism is introduced to describe the excitation of electrical eddy currents due to a time-varying magnetic field. The process works by applying a quasistatic approximation to Ampere's law and then segregating the magnetic field into impressed and induced terms. The result is a nonhomogeneous vector Helmholtz equation that can be analytically solved for many practical geometries. Four demonstration cases are then solved under a constant excitation field over all space—an infinite slab in one dimension, a longitudinal cylinder in two dimensions, a transverse cylinder in two dimensions, and a sphere in three dimensions. Numerical simulations are also performed in parallel with analytic computations, all of which verify the accuracy of the derived expressions.},
doi = {10.1109/MAP.2017.2774206},
journal = {IEEE Antennas and Propagation Magazine},
number = 1,
volume = 60,
place = {United States},
year = {Fri Dec 22 00:00:00 EST 2017},
month = {Fri Dec 22 00:00:00 EST 2017}
}
Web of Science
Figures / Tables:
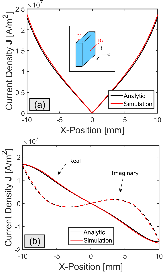 Fig. 1: (a) Current density magnitude |Jy(x)| along a thin metal slab with 2ℓ = 20 mm and σ = 1.0 MS/m. (b) Real and imaginary components of Jy(x).
Fig. 1: (a) Current density magnitude |Jy(x)| along a thin metal slab with 2ℓ = 20 mm and σ = 1.0 MS/m. (b) Real and imaginary components of Jy(x).
Figures / Tables found in this record:

 Search WorldCat to find libraries that may hold this journal
Search WorldCat to find libraries that may hold this journal