Modeling flow and transport in fracture networks using graphs
Abstract
Fractures form the main pathways for flow in the subsurface within low-permeability rock. For this reason, accurately predicting flow and transport in fractured systems is vital for improving the performance of subsurface applications. Fracture sizes in these systems can range from millimeters to kilometers. Although modeling flow and transport using the discrete fracture network (DFN) approach is known to be more accurate due to incorporation of the detailed fracture network structure over continuum-based methods, capturing the flow and transport in such a wide range of scales is still computationally intractable. Furthermore, if one has to quantify uncertainty, hundreds of realizations of these DFN models have to be run. To reduce the computational burden, we solve flow and transport on a graph representation of a DFN. We study the accuracy of the graph approach by comparing breakthrough times and tracer particle statistical data between the graph-based and the high-fidelity DFN approaches, for fracture networks with varying number of fractures and degree of heterogeneity. Due to our recent developments in capabilities to perform DFN high-fidelity simulations on fracture networks with large number of fractures, we are in a unique position to perform such a comparison. We show that the graph approach showsmore »
- Authors:
-
- Los Alamos National Laboratory (LANL), Los Alamos, NM (United States)
- Publication Date:
- Research Org.:
- Los Alamos National Laboratory (LANL), Los Alamos, NM (United States)
- Sponsoring Org.:
- USDOE
- OSTI Identifier:
- 1427375
- Alternate Identifier(s):
- OSTI ID: 1425242
- Report Number(s):
- LA-UR-17-25905
Journal ID: 2470-0045 ; 2470-0053 (Electronic)
- Grant/Contract Number:
- AC52-06NA25396; 20170103DR
- Resource Type:
- Accepted Manuscript
- Journal Name:
- Physical Review E
- Additional Journal Information:
- Journal Volume: 97; Journal Issue: 3
- Country of Publication:
- United States
- Language:
- English
- Subject:
- 58 GEOSCIENCES; 97 MATHEMATICS AND COMPUTING; Earth Sciences; Mathematics; subsurface, flow, transport, graph theory, fractures, breakthrough, particle tracking
Citation Formats
Karra, S., O'Malley, D., Hyman, J. D., Viswanathan, H. S., and Srinivasan, G. Modeling flow and transport in fracture networks using graphs. United States: N. p., 2018.
Web. doi:10.1103/PhysRevE.97.033304.
Karra, S., O'Malley, D., Hyman, J. D., Viswanathan, H. S., & Srinivasan, G. Modeling flow and transport in fracture networks using graphs. United States. https://doi.org/10.1103/PhysRevE.97.033304
Karra, S., O'Malley, D., Hyman, J. D., Viswanathan, H. S., and Srinivasan, G. Fri .
"Modeling flow and transport in fracture networks using graphs". United States. https://doi.org/10.1103/PhysRevE.97.033304. https://www.osti.gov/servlets/purl/1427375.
@article{osti_1427375,
title = {Modeling flow and transport in fracture networks using graphs},
author = {Karra, S. and O'Malley, D. and Hyman, J. D. and Viswanathan, H. S. and Srinivasan, G.},
abstractNote = {Fractures form the main pathways for flow in the subsurface within low-permeability rock. For this reason, accurately predicting flow and transport in fractured systems is vital for improving the performance of subsurface applications. Fracture sizes in these systems can range from millimeters to kilometers. Although modeling flow and transport using the discrete fracture network (DFN) approach is known to be more accurate due to incorporation of the detailed fracture network structure over continuum-based methods, capturing the flow and transport in such a wide range of scales is still computationally intractable. Furthermore, if one has to quantify uncertainty, hundreds of realizations of these DFN models have to be run. To reduce the computational burden, we solve flow and transport on a graph representation of a DFN. We study the accuracy of the graph approach by comparing breakthrough times and tracer particle statistical data between the graph-based and the high-fidelity DFN approaches, for fracture networks with varying number of fractures and degree of heterogeneity. Due to our recent developments in capabilities to perform DFN high-fidelity simulations on fracture networks with large number of fractures, we are in a unique position to perform such a comparison. We show that the graph approach shows a consistent bias with up to an order of magnitude slower breakthrough when compared to the DFN approach. We show that this is due to graph algorithm's underprediction of the pressure gradients across intersections on a given fracture, leading to slower tracer particle speeds between intersections and longer travel times. We present a bias correction methodology to the graph algorithm that reduces the discrepancy between the DFN and graph predictions. We show that with this bias correction, the graph algorithm predictions significantly improve and the results are very accurate. In conclusion, the good accuracy and the low computational cost, with O(104) times lower times than the DFN, makes the graph algorithm an ideal technique to incorporate in uncertainty quantification methods.},
doi = {10.1103/PhysRevE.97.033304},
journal = {Physical Review E},
number = 3,
volume = 97,
place = {United States},
year = {Fri Mar 09 00:00:00 EST 2018},
month = {Fri Mar 09 00:00:00 EST 2018}
}
Web of Science
Figures / Tables:
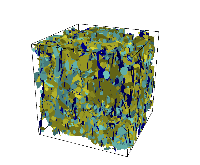 Figure-1: Discrete fracture network made up of 6330 circular fracture whose radii are sampled from three independent truncated power-law distributions. Fractures are colored by family. There are about 13 million grid cells in this model.
Figure-1: Discrete fracture network made up of 6330 circular fracture whose radii are sampled from three independent truncated power-law distributions. Fractures are colored by family. There are about 13 million grid cells in this model.
Works referenced in this record:
Effect of transport-pathway simplifications on projected releases of radionuclides from a nuclear waste repository (Sweden)
journal, August 2012
- Selroos, Jan-Olof; Painter, Scott L.
- Hydrogeology Journal, Vol. 20, Issue 8
A Model for Investigating Mechanical Transport in Fracture Networks
journal, October 1984
- Endo, H. K.; Long, J. C. S.; Wilson, C. R.
- Water Resources Research, Vol. 20, Issue 10
On Simulations of Discrete Fracture Network Flows with an Optimization-Based Extended Finite Element Method
journal, January 2013
- Berrone, Stefano; Pieraccini, Sandra; Scialò, Stefano
- SIAM Journal on Scientific Computing, Vol. 35, Issue 2
Topology of fracture networks
journal, January 2013
- Andresen, Christian André; Hansen, Alex; Le Goc, Romain
- Frontiers in Physics, Vol. 1
Theory of anomalous chemical transport in random fracture networks
journal, May 1998
- Berkowitz, Brian; Scher, Harvey
- Physical Review E, Vol. 57, Issue 5
Dispersion in tracer flow in fractured geothermal systems
journal, April 1983
- Horne, Roland N.; Rodriguez, Fernando
- Geophysical Research Letters, Vol. 10, Issue 4
Anomalous Transport in Random Fracture Networks
journal, November 1997
- Berkowitz, Brian; Scher, Harvey
- Physical Review Letters, Vol. 79, Issue 20
Modeling fracture flow with a stochastic discrete fracture network: calibration and validation: 1. The flow model
journal, March 1990
- Cacas, M. C.; Ledoux, E.; de Marsily, G.
- Water Resources Research, Vol. 26, Issue 3
A descriptive study of fracture networks in rocks using complex network metrics
journal, March 2016
- Santiago, Elizabeth; Velasco-Hernández, Jorge X.; Romero-Salcedo, Manuel
- Computers & Geosciences, Vol. 88
Upscaling discrete fracture network simulations: An alternative to continuum transport models: UPSCALING FRACTURE NETWORK SIMULATIONS
journal, February 2005
- Painter, S.; Cvetkovic, V.
- Water Resources Research, Vol. 41, Issue 2
Particle tracking approach for transport in three-dimensional discrete fracture networks: Particle tracking in 3-D DFNs
journal, September 2015
- Makedonska, Nataliia; Painter, Scott L.; Bui, Quan M.
- Computational Geosciences, Vol. 19, Issue 5
Numerical methods for reactive transport on rectangular and streamline-oriented grids
journal, April 1999
- Cirpka, Olaf A.; Frind, Emil O.; Helmig, Rainer
- Advances in Water Resources, Vol. 22, Issue 7
Predictions of first passage times in sparse discrete fracture networks using graph-based reductions
journal, July 2017
- Hyman, Jeffrey D.; Hagberg, Aric; Srinivasan, Gowri
- Physical Review E, Vol. 96, Issue 1
Fracture size and transmissivity correlations: Implications for transport simulations in sparse three-dimensional discrete fracture networks following a truncated power law distribution of fracture size: FRACTURE SIZE AND TRANSMISSIVITY CORRELATIONS
journal, August 2016
- Hyman, J. D.; Aldrich, G.; Viswanathan, H.
- Water Resources Research, Vol. 52, Issue 8
A stochastic analysis of macroscopic dispersion in fractured media
journal, October 1983
- Schwartz, Franklin W.; Smith, Leslie; Crowe, Allan S.
- Water Resources Research, Vol. 19, Issue 5
Effect of advective flow in fractures and matrix diffusion on natural gas production
journal, October 2015
- Karra, Satish; Makedonska, Nataliia; Viswanathan, Hari S.
- Water Resources Research, Vol. 51, Issue 10
dfnWorks: A discrete fracture network framework for modeling subsurface flow and transport
journal, November 2015
- Hyman, Jeffrey D.; Karra, Satish; Makedonska, Nataliia
- Computers & Geosciences, Vol. 84
A Generalized Mixed Hybrid Mortar Method for Solving Flow in Stochastic Discrete Fracture Networks
journal, January 2012
- Pichot, G.; Erhel, J.; de Dreuzy, J. -R.
- SIAM Journal on Scientific Computing, Vol. 34, Issue 1
The “small-world” topology of rock fracture networks
journal, April 2007
- Valentini, Luca; Perugini, Diego; Poli, Giampiero
- Physica A: Statistical Mechanics and its Applications, Vol. 377, Issue 1
Large-Scale Optimization-Based Non-negative Computational Framework for Diffusion Equations: Parallel Implementation and Performance Studies
journal, July 2016
- Chang, J.; Karra, S.; Nakshatrala, K. B.
- Journal of Scientific Computing, Vol. 70, Issue 1
The random walk's guide to anomalous diffusion: a fractional dynamics approach
journal, December 2000
- Metzler, Ralf; Klafter, Joseph
- Physics Reports, Vol. 339, Issue 1
Conforming Delaunay Triangulation of Stochastically Generated Three Dimensional Discrete Fracture Networks: A Feature Rejection Algorithm for Meshing Strategy
journal, January 2014
- Hyman, Jeffrey D.; Gable, Carl W.; Painter, Scott L.
- SIAM Journal on Scientific Computing, Vol. 36, Issue 4
Scaling of fracture systems in geological media
journal, August 2001
- Bonnet, E.; Bour, O.; Odling, N. E.
- Reviews of Geophysics, Vol. 39, Issue 3
Characterizing flow and transport in fractured geological media: A review
journal, August 2002
- Berkowitz, Brian
- Advances in Water Resources, Vol. 25, Issue 8-12
Analysis of weighted networks
journal, November 2004
- Newman, M. E. J.
- Physical Review E, Vol. 70, Issue 5
A monotone finite volume method for advection–diffusion equations on unstructured polygonal meshes
journal, June 2010
- Lipnikov, K.; Svyatskiy, D.; Vassilevski, Y.
- Journal of Computational Physics, Vol. 229, Issue 11
Pathline tracing on fully unstructured control-volume grids
journal, July 2012
- Painter, S. L.; Gable, C. W.; Kelkar, S.
- Computational Geosciences, Vol. 16, Issue 4
Uncertainty in Prediction of Radionuclide Gas Migration from Underground Nuclear Explosions
journal, January 2014
- Jordan, Amy B.; Stauffer, Philip H.; Zyvoloski, George A.
- Vadose Zone Journal, Vol. 13, Issue 10
Works referencing / citing this record:
Robust system size reduction of discrete fracture networks: a multi-fidelity method that preserves transport characteristics
journal, September 2018
- Srinivasan, Shriram; Hyman, Jeffrey; Karra, Satish
- Computational Geosciences, Vol. 22, Issue 6
Model reduction for fractured porous media: a machine learning approach for identifying main flow pathways
journal, March 2019
- Srinivasan, Shriram; Karra, Satish; Hyman, Jeffrey
- Computational Geosciences, Vol. 23, Issue 3
Partitioning Dynamics of Gravity‐Driven Unsaturated Flow Through Simple T‐Shaped Fracture Intersections
journal, August 2019
- Yang, Zhibing; Xue, Song; Zheng, Xiaokang
- Water Resources Research, Vol. 55, Issue 8
Quantifying Topological Uncertainty in Fractured Systems using Graph Theory and Machine Learning
journal, August 2018
- Srinivasan, Gowri; Hyman, Jeffrey D.; Osthus, David A.
- Scientific Reports, Vol. 8, Issue 1
Figures / Tables found in this record:

 Search WorldCat to find libraries that may hold this journal
Search WorldCat to find libraries that may hold this journal