Non-axisymmetric Aberration Patterns from Wide-field Telescopes Using Spin-weighted Zernike Polynomials
Abstract
If the optical system of a telescope is perturbed from rotational symmetry, the Zernike wavefront aberration coefficients describing that system can be expressed as a function of position in the focal plane using spin-weighted Zernike polynomials. Methodologies are presented to derive these polynomials to arbitrary order. This methodology is applied to aberration patterns produced by a misaligned Ritchey Chretian telescope and to distortion patterns at the focal plane of the DESI optical corrector, where it is shown to provide a more efficient description of distortion than conventional expansions.
- Authors:
-
- Fermi National Accelerator Lab. (FNAL), Batavia, IL (United States)
- Publication Date:
- Research Org.:
- Fermi National Accelerator Lab. (FNAL), Batavia, IL (United States)
- Sponsoring Org.:
- USDOE Office of Science (SC), High Energy Physics (HEP)
- Contributing Org.:
- DESI
- OSTI Identifier:
- 1409339
- Report Number(s):
- FERMILAB-PUB-17-508-AE-CD; arXiv:1711.03916
Journal ID: ISSN 0004-6280; 1637059
- Grant/Contract Number:
- AC02-07CH11359
- Resource Type:
- Accepted Manuscript
- Journal Name:
- Publications of the Astronomical Society of the Pacific
- Additional Journal Information:
- Journal Volume: 130; Journal Issue: 986; Journal ID: ISSN 0004-6280
- Publisher:
- Astronomical Society of the Pacific
- Country of Publication:
- United States
- Language:
- English
- Subject:
- 79 ASTRONOMY AND ASTROPHYSICS; methods analytical; telescopes
Citation Formats
Kent, Stephen M. Non-axisymmetric Aberration Patterns from Wide-field Telescopes Using Spin-weighted Zernike Polynomials. United States: N. p., 2018.
Web. doi:10.1088/1538-3873/aaa6b8.
Kent, Stephen M. Non-axisymmetric Aberration Patterns from Wide-field Telescopes Using Spin-weighted Zernike Polynomials. United States. https://doi.org/10.1088/1538-3873/aaa6b8
Kent, Stephen M. Thu .
"Non-axisymmetric Aberration Patterns from Wide-field Telescopes Using Spin-weighted Zernike Polynomials". United States. https://doi.org/10.1088/1538-3873/aaa6b8. https://www.osti.gov/servlets/purl/1409339.
@article{osti_1409339,
title = {Non-axisymmetric Aberration Patterns from Wide-field Telescopes Using Spin-weighted Zernike Polynomials},
author = {Kent, Stephen M.},
abstractNote = {If the optical system of a telescope is perturbed from rotational symmetry, the Zernike wavefront aberration coefficients describing that system can be expressed as a function of position in the focal plane using spin-weighted Zernike polynomials. Methodologies are presented to derive these polynomials to arbitrary order. This methodology is applied to aberration patterns produced by a misaligned Ritchey Chretian telescope and to distortion patterns at the focal plane of the DESI optical corrector, where it is shown to provide a more efficient description of distortion than conventional expansions.},
doi = {10.1088/1538-3873/aaa6b8},
journal = {Publications of the Astronomical Society of the Pacific},
number = 986,
volume = 130,
place = {United States},
year = {Thu Feb 15 00:00:00 EST 2018},
month = {Thu Feb 15 00:00:00 EST 2018}
}
Free Publicly Available Full Text
Publisher's Version of Record
Other availability
Search WorldCat to find libraries that may hold this journal
Cited by: 5 works
Citation information provided by
Web of Science
Web of Science
Figures / Tables:
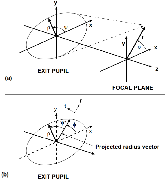Figure 1: (a) Schematic diagram showing the orientation and coordinate system definitions of the pupil plane ($ρ, ψ$) and focal plane ($r, \phi$). Each point in the focal plane (e.g., at radius vector $\bar{r}$) sees an image of the exit pupil. A global Cartesian ($x, y$) system is illustrated. (b)more »
All figures and tables
(10 total)
Save to My Library
You must Sign In or Create an Account in order to save documents to your library.
Figures/Tables have been extracted from DOE-funded journal article accepted manuscripts.