Information-entropic signature of the critical point
Abstract
Here, we investigate the critical behavior of continuous (second-order) phase transitions in the context of (2 + 1)-dimensional Ginzburg–Landau models with a double-well effective potential. In particular, we show that the recently-proposed configurational entropy (CE)—a measure of the spatial complexity of the order parameter in momentum space based on its Fourier-mode decomposition—can be used to identify the critical point. We compute the CE for different temperatures and show that large spatial fluctuations near the critical point (Tc)—characterized by a divergent correlation length—lead to a sharp decrease in the associated configurational entropy. We further show that the CE density goes from a scale-free to an approximate scaling behavior |k|–5/3 as the critical point is approached. As a result, we reproduce the behavior of the CE at criticality with a percolating many-bubble model.
- Authors:
- Publication Date:
- Research Org.:
- Dartmouth College, Hanover, NH (United States)
- Sponsoring Org.:
- USDOE
- OSTI Identifier:
- 1209772
- Alternate Identifier(s):
- OSTI ID: 1457029
- Grant/Contract Number:
- SC0010386; 48038
- Resource Type:
- Published Article
- Journal Name:
- Physics Letters B
- Additional Journal Information:
- Journal Name: Physics Letters B Journal Volume: 747 Journal Issue: C; Journal ID: ISSN 0370-2693
- Publisher:
- Elsevier
- Country of Publication:
- Netherlands
- Language:
- English
- Subject:
- 71 CLASSICAL AND QUANTUM MECHANICS, GENERAL PHYSICS; 97 MATHEMATICS AND COMPUTING
Citation Formats
Gleiser, Marcelo, and Sowinski, Damian. Information-entropic signature of the critical point. Netherlands: N. p., 2015.
Web. doi:10.1016/j.physletb.2015.05.058.
Gleiser, Marcelo, & Sowinski, Damian. Information-entropic signature of the critical point. Netherlands. https://doi.org/10.1016/j.physletb.2015.05.058
Gleiser, Marcelo, and Sowinski, Damian. Wed .
"Information-entropic signature of the critical point". Netherlands. https://doi.org/10.1016/j.physletb.2015.05.058.
@article{osti_1209772,
title = {Information-entropic signature of the critical point},
author = {Gleiser, Marcelo and Sowinski, Damian},
abstractNote = {Here, we investigate the critical behavior of continuous (second-order) phase transitions in the context of (2 + 1)-dimensional Ginzburg–Landau models with a double-well effective potential. In particular, we show that the recently-proposed configurational entropy (CE)—a measure of the spatial complexity of the order parameter in momentum space based on its Fourier-mode decomposition—can be used to identify the critical point. We compute the CE for different temperatures and show that large spatial fluctuations near the critical point (Tc)—characterized by a divergent correlation length—lead to a sharp decrease in the associated configurational entropy. We further show that the CE density goes from a scale-free to an approximate scaling behavior |k|–5/3 as the critical point is approached. As a result, we reproduce the behavior of the CE at criticality with a percolating many-bubble model.},
doi = {10.1016/j.physletb.2015.05.058},
journal = {Physics Letters B},
number = C,
volume = 747,
place = {Netherlands},
year = {Wed Jul 01 00:00:00 EDT 2015},
month = {Wed Jul 01 00:00:00 EDT 2015}
}
Free Publicly Available Full Text
Publisher's Version of Record
https://doi.org/10.1016/j.physletb.2015.05.058
https://doi.org/10.1016/j.physletb.2015.05.058
Other availability
Search WorldCat to find libraries that may hold this journal
Cited by: 46 works
Citation information provided by
Web of Science
Web of Science
Figures / Tables:
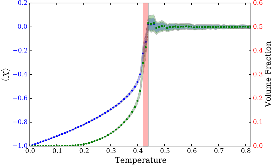Fig. 1: (Color online.) The order parameter 〈X〉 [top (blue) line] and the volume fraction (pV ) occupied by the X > 0 phase [bottom (green) line] vs. temperature. The shaded regions correspond to 1σ deviations from the mean. Within the accuracy of our simulation, the critical temperature is θcmore »
All figures and tables
(5 total)
Save to My Library
You must Sign In or Create an Account in order to save documents to your library.
Works referenced in this record:
A Mathematical Theory of Communication
journal, July 1948
- Shannon, C. E.
- Bell System Technical Journal, Vol. 27, Issue 3
Information-entropic stability bound for compact objects: Application to Q-balls and the Chandrasekhar limit of polytropes
journal, November 2013
- Gleiser, Marcelo; Sowinski, Damian
- Physics Letters B, Vol. 727, Issue 1-3
Matching numerical simulations to continuum field theories: A lattice renormalization study
journal, January 1997
- Borrill, Julian; Gleiser, Marcelo
- Nuclear Physics B, Vol. 483, Issue 1-2
On thermalization in classical scalar field theory
journal, October 2000
- Aarts, Gert; Bonini, Gian Franco; Wetterich, Christof
- Nuclear Physics B, Vol. 587, Issue 1-3
Entropic measure for localized energy configurations: Kinks, bounces, and bubbles
journal, July 2012
- Gleiser, Marcelo; Stamatopoulos, Nikitas
- Physics Letters B, Vol. 713, Issue 3
A Mathematical Theory of Communication
journal, October 1948
- Shannon, C. E.
- Bell System Technical Journal, Vol. 27, Issue 4
Configurational entropy elucidates the role of salt-bridge networks in protein thermostability
journal, July 2007
- Missimer, John H.; Steinmetz, Michel O.; Baron, Riccardo
- Protein Science, Vol. 16, Issue 7
Scale-space for discrete signals
journal, March 1990
- Lindeberg, T.
- IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 12, Issue 3
Nonperturbative dynamics of reheating after inflation: A review
journal, December 2014
- Amin, Mustafa A.; Hertzberg, Mark P.; Kaiser, David I.
- International Journal of Modern Physics D, Vol. 24, Issue 01
Exact and truncated dynamics in nonequilibrium field theory
journal, December 2000
- Aarts, Gert; Bonini, Gian Franco; Wetterich, Christof
- Physical Review D, Vol. 63, Issue 2
Transition to order after hilltop inflation
journal, March 2014
- Gleiser, Marcelo; Graham, Noah
- Physical Review D, Vol. 89, Issue 8
Information content of spontaneous symmetry breaking
journal, August 2012
- Gleiser, Marcelo; Stamatopoulos, Nikitas
- Physical Review D, Vol. 86, Issue 4
Figures / Tables found in this record:
Figures/Tables have been extracted from DOE-funded journal article accepted manuscripts.