Bond percolation thresholds on Archimedean lattices from critical polynomial roots
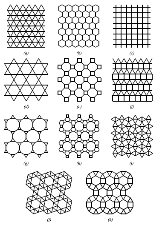
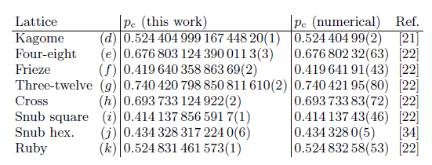
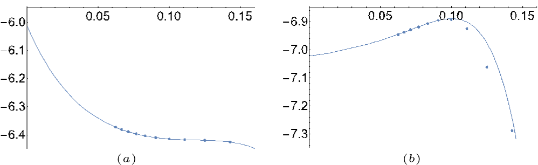
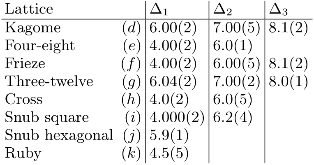
We present percolation thresholds calculated numerically with the eigenvalue formulation of the method of critical polynomials; developed in the last few years, it has already proven to be orders of magnitude more accurate than traditional techniques. Here, we report the result of large parallel calculations to produce what we believe may become the reference values of bond percolation thresholds on the Archimedean lattices for years to come. For example, for the kagome lattice we find pc= 0.524 404 999 167 448 20 (1) , whereas the best estimate using standard techniques is pc= 0.524 404 99 (2) . We further provide strong evidence that there are two classes of lattices: one for which the first three scaling exponents characterizing the finite-size corrections to pc are Δ = 6, 7, 8 , and another for which Δ = 4, 6, 8. We discuss the open questions related to the method, such as the full scaling law, as well as its potential for determining the critical points of other models.
- Research Organization:
- Lawrence Livermore National Laboratory (LLNL), Livermore, CA (United States)
- Sponsoring Organization:
- USDOE National Nuclear Security Administration (NNSA); USDOE Laboratory Directed Research and Development (LDRD) Program
- Grant/Contract Number:
- AC52-07NA27344; 19-DR-013
- OSTI ID:
- 1602370
- Alternate ID(s):
- OSTI ID: 1670554
- Report Number(s):
- LLNL-JRNL-795621; PPRHAI; 012050
- Journal Information:
- Physical Review Research, Journal Name: Physical Review Research Vol. 2 Journal Issue: 1; ISSN 2643-1564
- Publisher:
- American Physical Society (APS)Copyright Statement
- Country of Publication:
- United States
- Language:
- English
Similar Records
Percolation critical polynomial as a graph invariant
Polynomial sequences for bond percolation critical thresholds