DOE R&D Accomplishments Retirement
DOE R&D Accomplishments is no longer being maintained as a stand-alone search product. However, users will be able to continue to get to the contents of DOE R&D Accomplishments within OSTI.GOV through a minimal number of extra steps.
Shorter search path:
- Go to https://www.osti.gov/search/nobel:true
- This will display all records in the Limit to Nobel Prize winning researchers only view.
- On the left of the screen, users will see some additional options to refine the results of the Nobel Prize winning researchers.
- In the top area, users can click on [modify your search].
- [modify this search] provides users the ability to edit the search query in the advanced search screen.
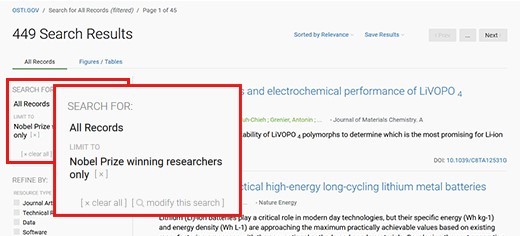
Figure 273508: R and D Accomplishments Nobel:true
Image renders screenshot of Nobel records search results.
Showing about 449 search results for Nobel records currently.
Another screenshot in the image emphasizes what filter criteria are applied:
Search for: All Records
Limit to: Nobel Prize winning researchers only
is shown when the link https://www.osti.gov/search/nobel:true is followed.
More detailed search path:
- Go to https://www.osti.gov
- Set the cursor on the down arrow in the main search box to see advanced search options.
- At the bottom of that box click on More Options.
- Scroll down to bottom of list and check: Limit to Nobel Prize winning researchers only.
- While in the advanced search, users may also enter other search criteria.
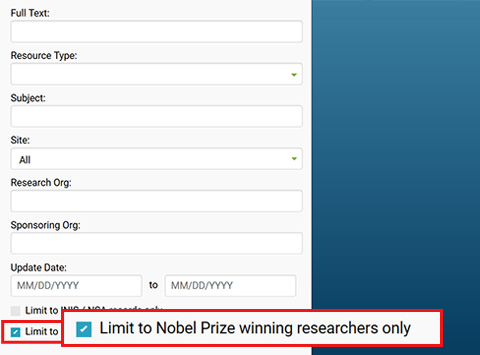
Figure 273509: R and D Accomplishments search path
Image showing screenshot of advanced search dropdown on OSTI homepage.
Highlights the "Limit to Nobel Prize winning researchers only" checkbox to search for Nobel records items.
This checkbox sits at end of the "More Options" fiters section.
Visit any of the OSTI search tools below to find Department of Energy R&D results.
Science, technology, and engineering research information funded by DOE
Scholarly scientific publications resulting from DOE-funded research
Scientific research data resulting from DOE-funded research
Open source, submission and search tool for DOE-funded software
Patents resulting from DOE-funded research
Scientific videos featuring DOE-funded research
U.S. government funded science information
Global science gateway


